Final Project - Practical StructCurves
Final Project Report
Formal Description of the Project
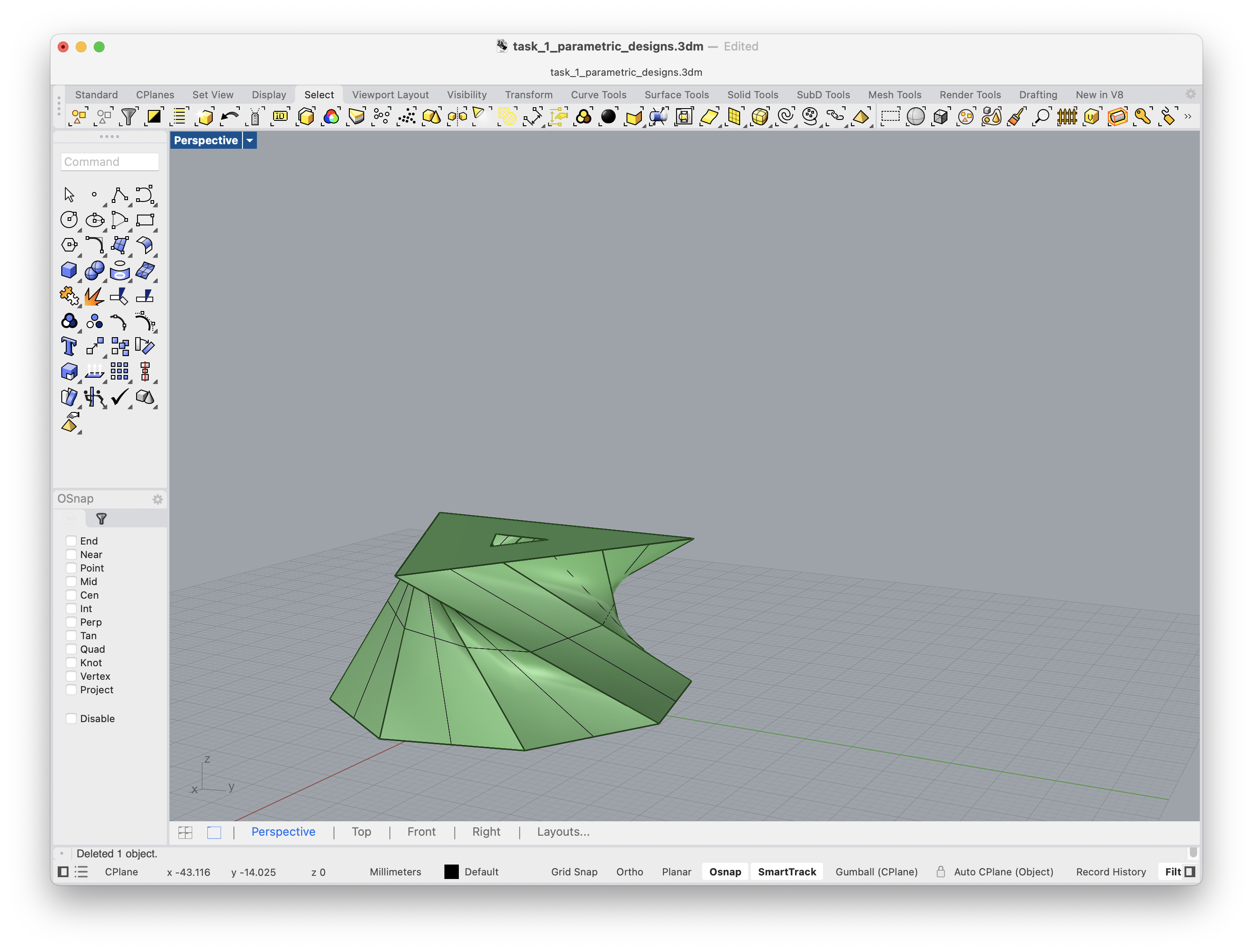
My goal with this project was to play around with the ideas of the StructCurves research paper from the “User Interface Software and Technology” (UIST) Conference in 2024. This led to me wanting to create zipper-like line structures made of blocks that join together and become rigid. The first approach was to play around with “prismatic” joints which slide into place, but don’t offer any significant resistance when pulled apart. The second approach was to change the joints to use “resolute” joints which use rotational characteristics to lock the zipper-like structure in. I chose to use a naive 3d approach where the 3rd axis (z) isn’t locked in so you can shift the blocks vertically. The setup uses Rhino and Grasshopper to export .stl files that get printed on a Bambu A1 Mini after being sliced in Bambu Studio.
The final code is located in my Github repo. The first draft of prismatic joints are the files prefixed prsmatic_joints, and the final resolute joint files are prefixed resolute_2d.
First Steps - Naive Prismatic Joints
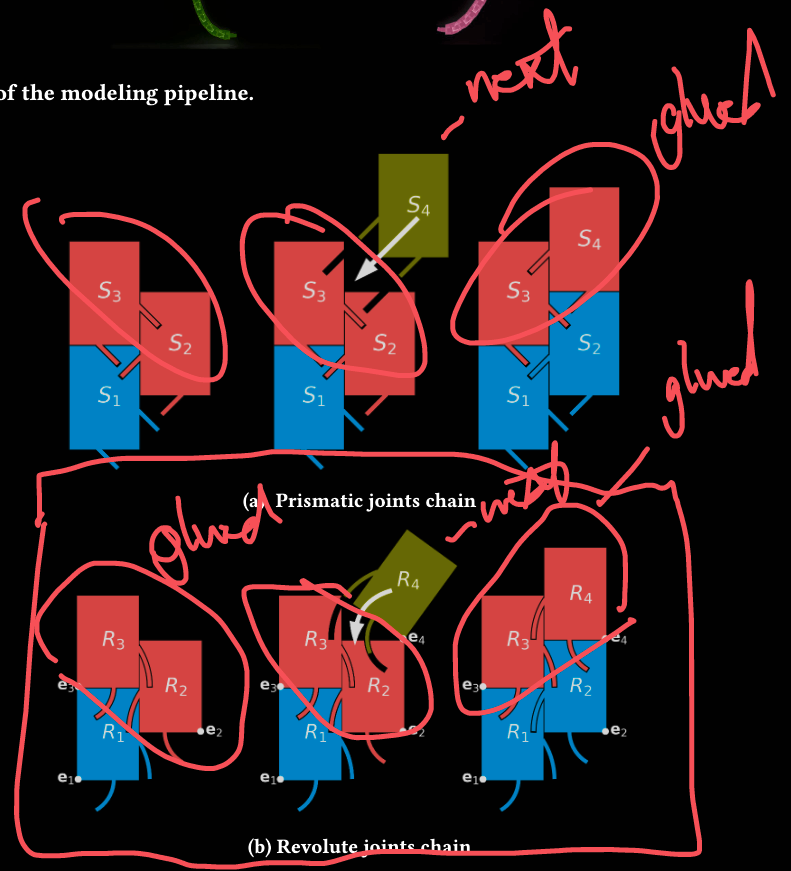
The first thing I decided to prototype was getting blocks to work with teeth set at 45 degree angles (the “prismatic” approach described in the paper).
The grasshopper code uses boxes to create the blocks, and the teeth are rotated boxes aligned to the two sides of the block. I would then bake the final blocks and print them.
This approach was naive because there was no offset for the teeth. This meant that the force of pushing the PLA blocks together worked if the blocks weren’t very thick, but would warp and not fit very well with higher height values.


Another quirk I hadn’t thought about was how the first layer gets compressed on the bed creating an “elephant foot” bulge. I’ve seen there are some other ways to try to fix this with higher bed temps or tweaking z-offsets, but I knew I’d need some space regardless and didn’t want to focus on that issue. This naive prismatic joint approach also meant the pieces slide into place easily, but also slide apart easily because the teeth don’t have any geometry holding things in place. Friction and top/bottom pieces being glued were the only approaches to lock these pieces in.
Second Steps - A Resolute Joints Approach
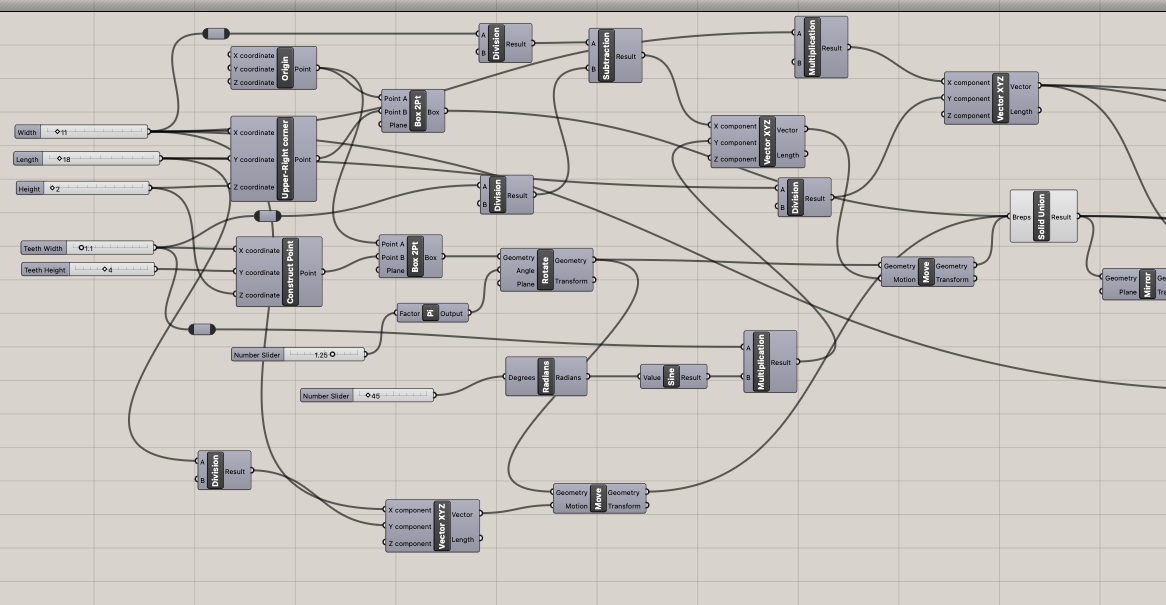
The next approach was to make sure that the teeth would curve and to add offsets. I decided to do this by building up the blocks from rectangles so I could offset them (instead of boxes) and then extrude the height I wanted my final blocks to be.
For parameters, I made sure I could change the block width, length, and height. I made it so I could change the spacing between the blocks to make it so the prints wouldn’t stick as well.
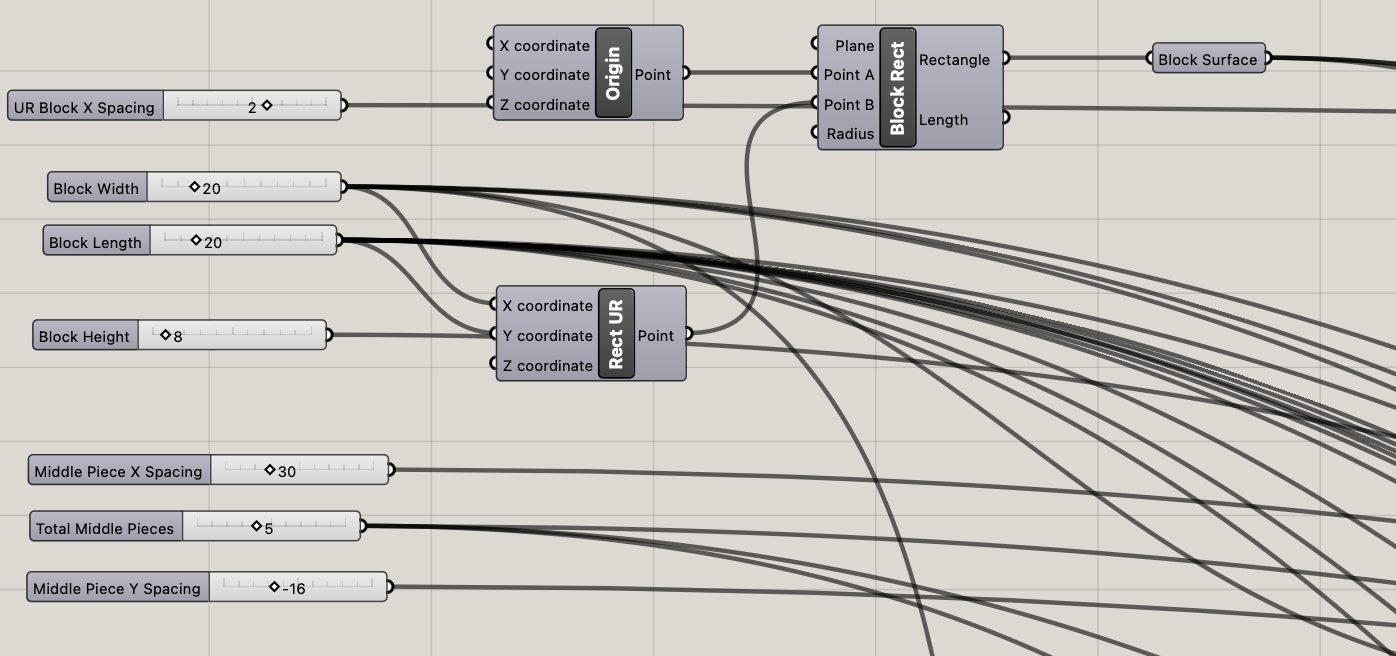
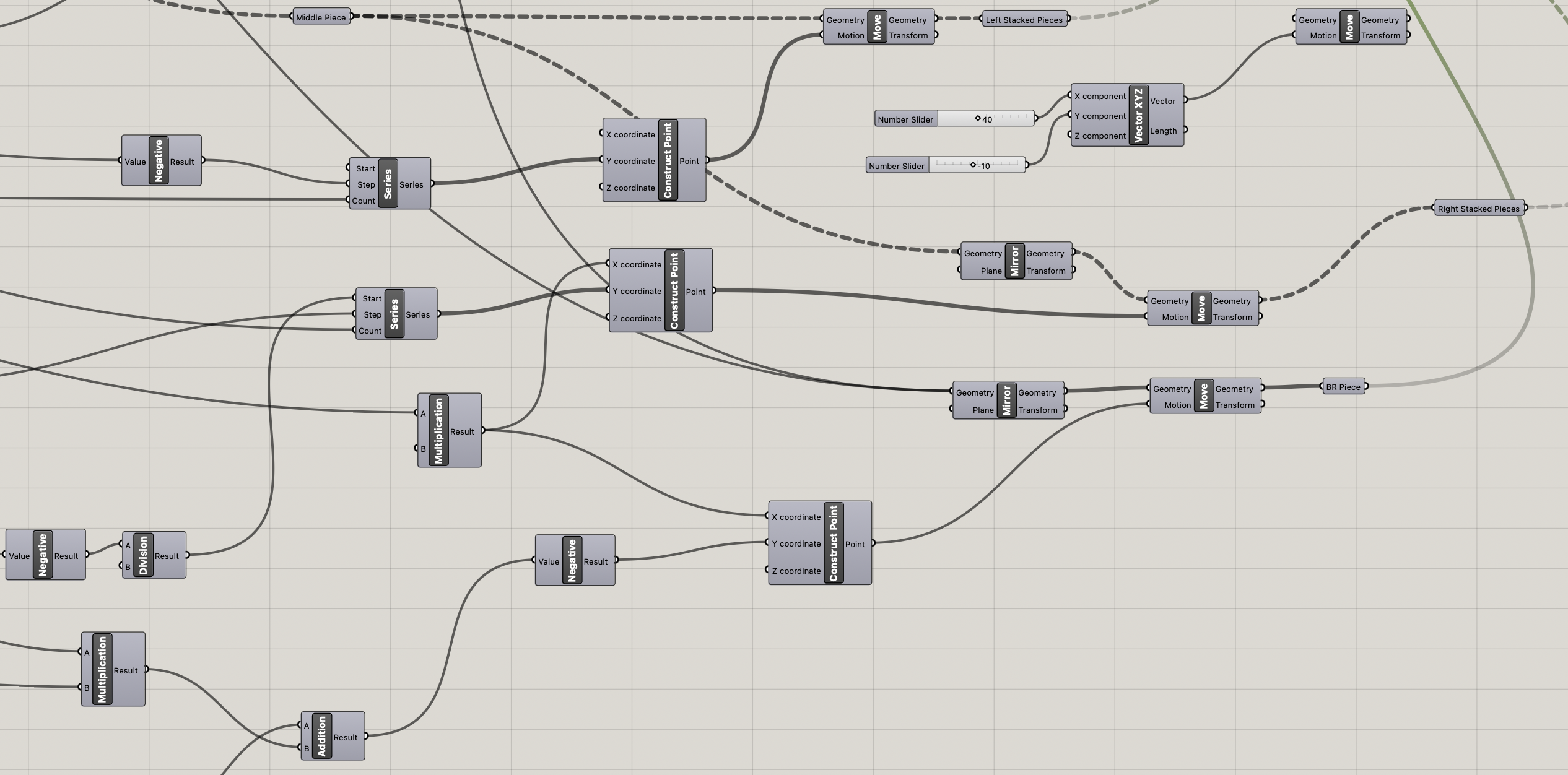
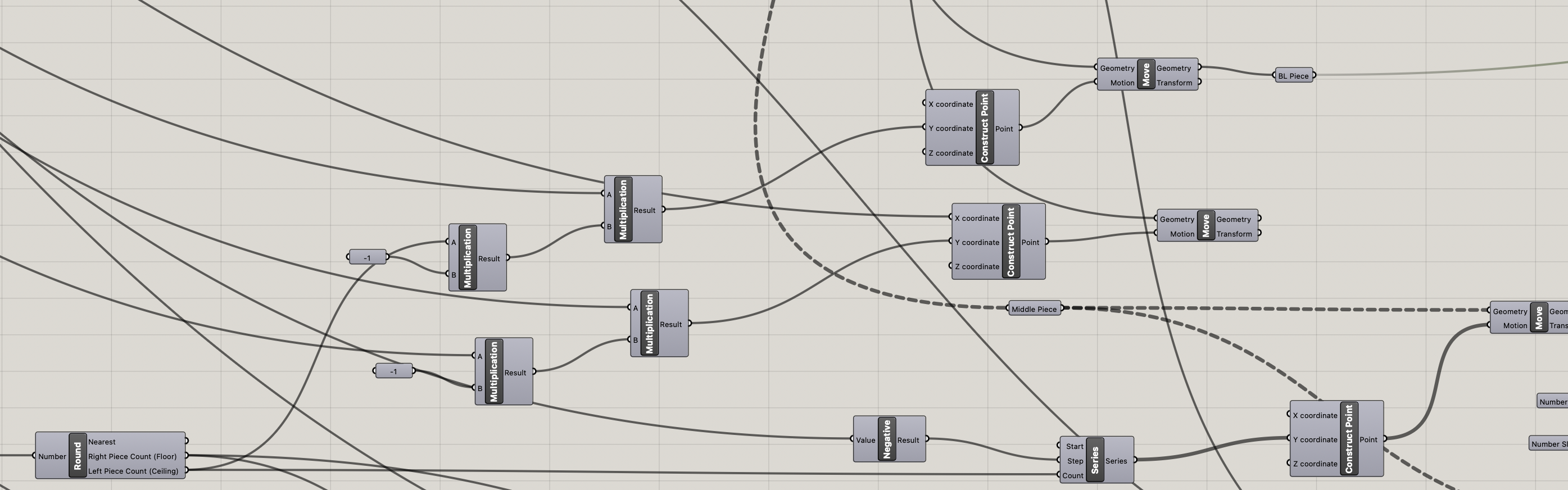
Parameters were added to adjust how the teeth aligned on the x/y axes of the block. The teeth get made by taking rectangles and using the flow component along with an arc.
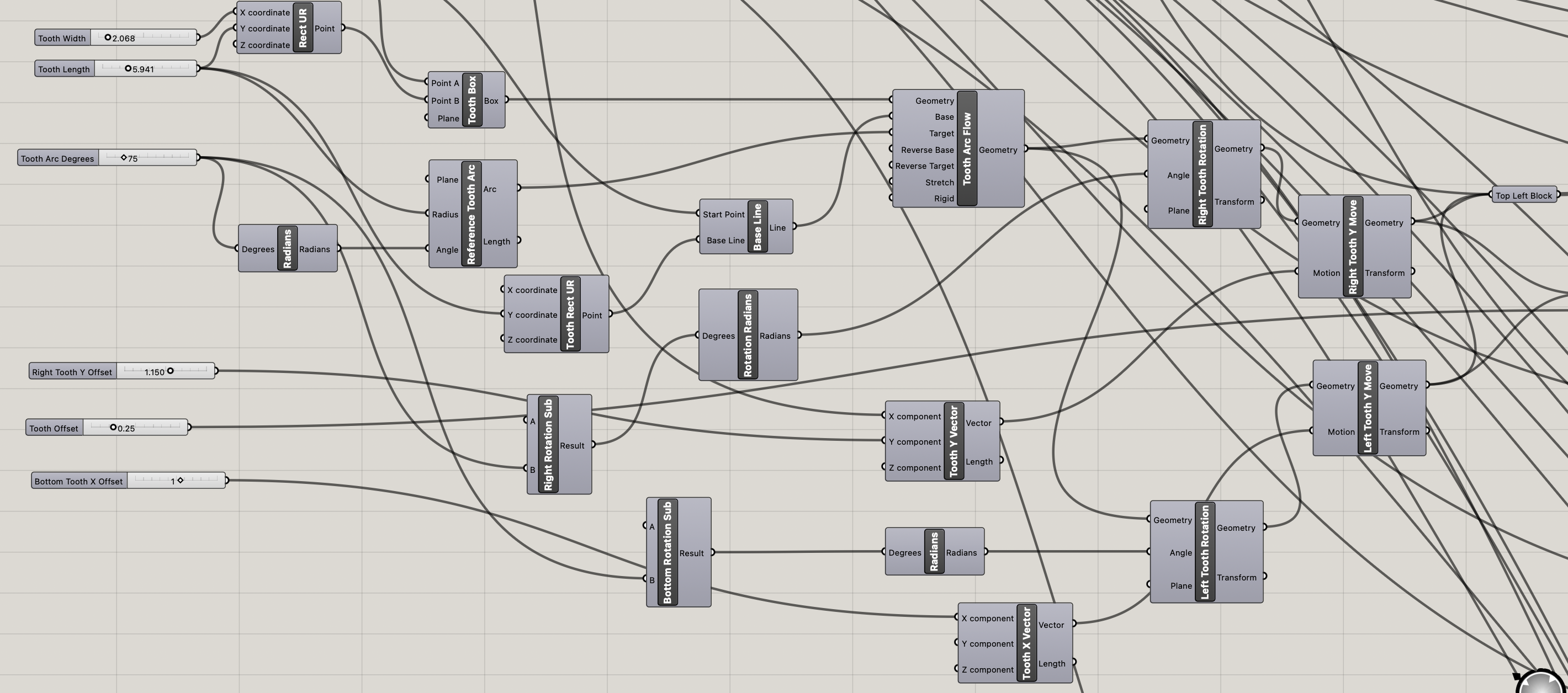
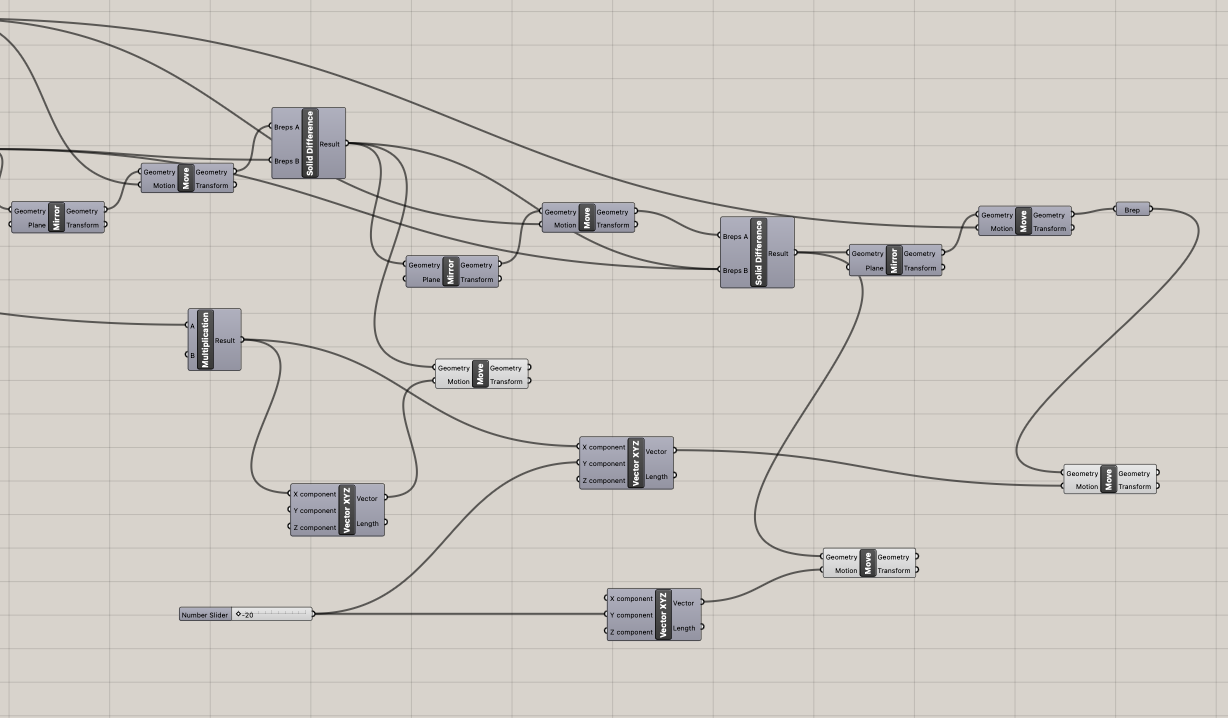
To make the rest of the blocks I moved blocks with the teeth and offsets and used solid differences and solid intersections to make new blocks with joint holes. In a lot of cases I also abused using mirror to get more blocks.
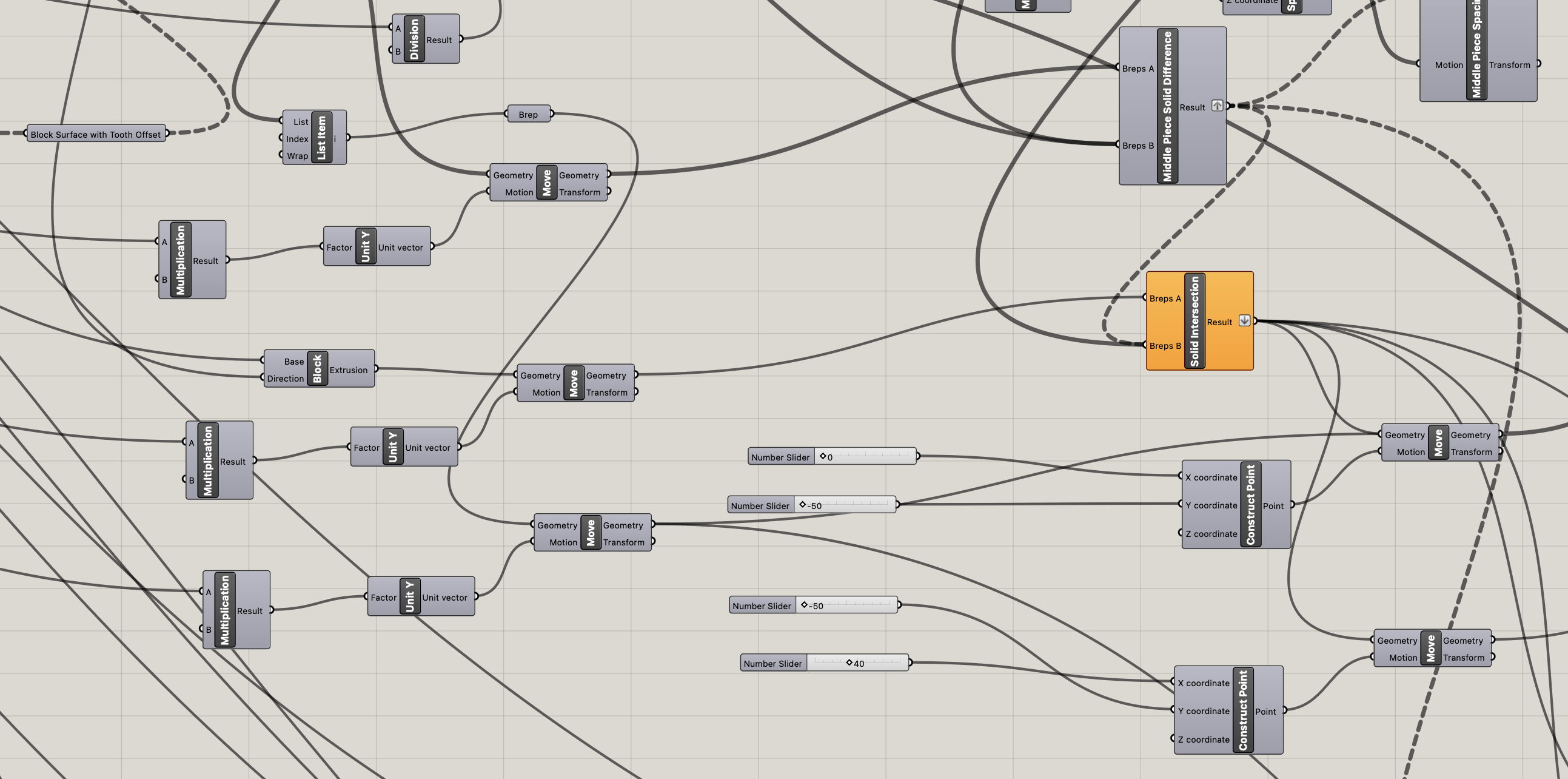
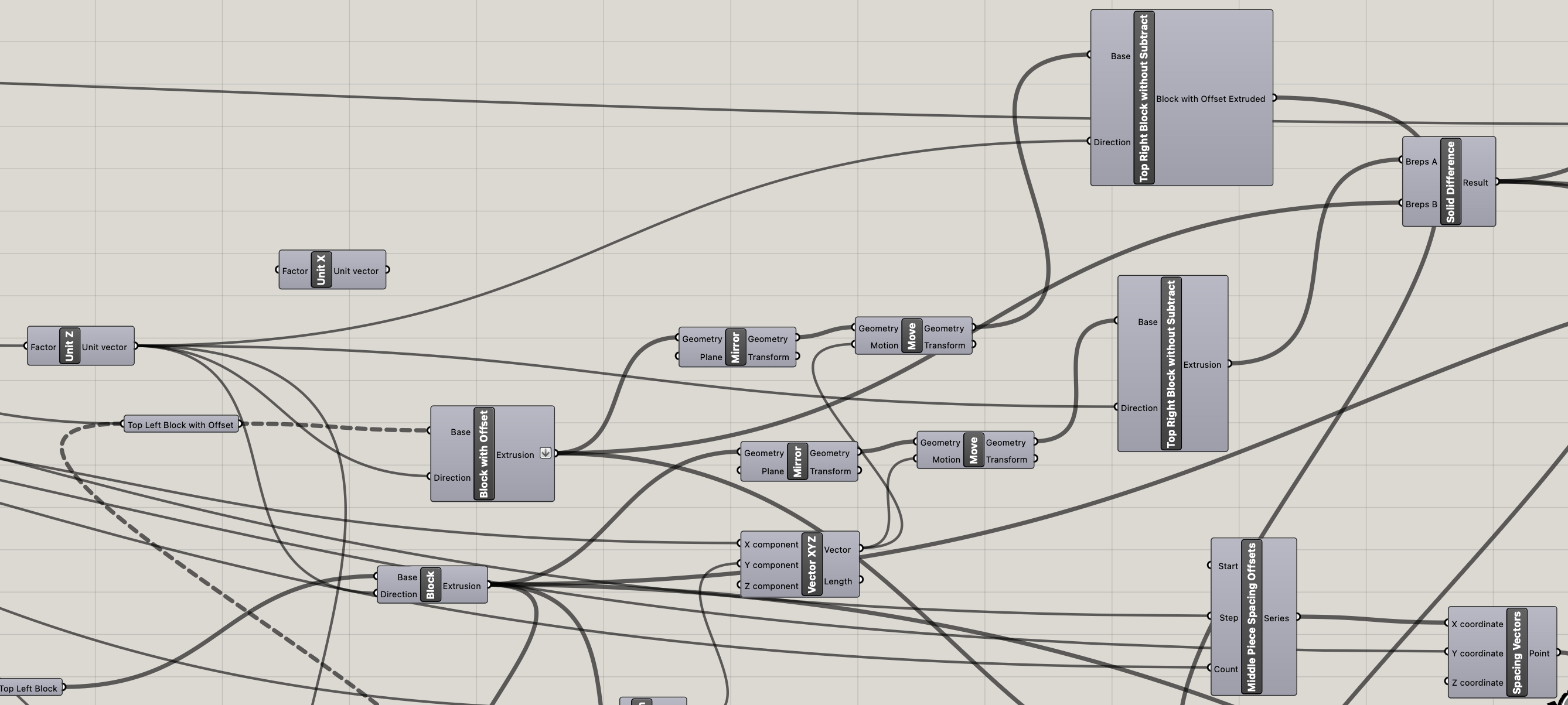
The final result is feeding all the block breps into a pancake component to export the final blocks to a .stl file.
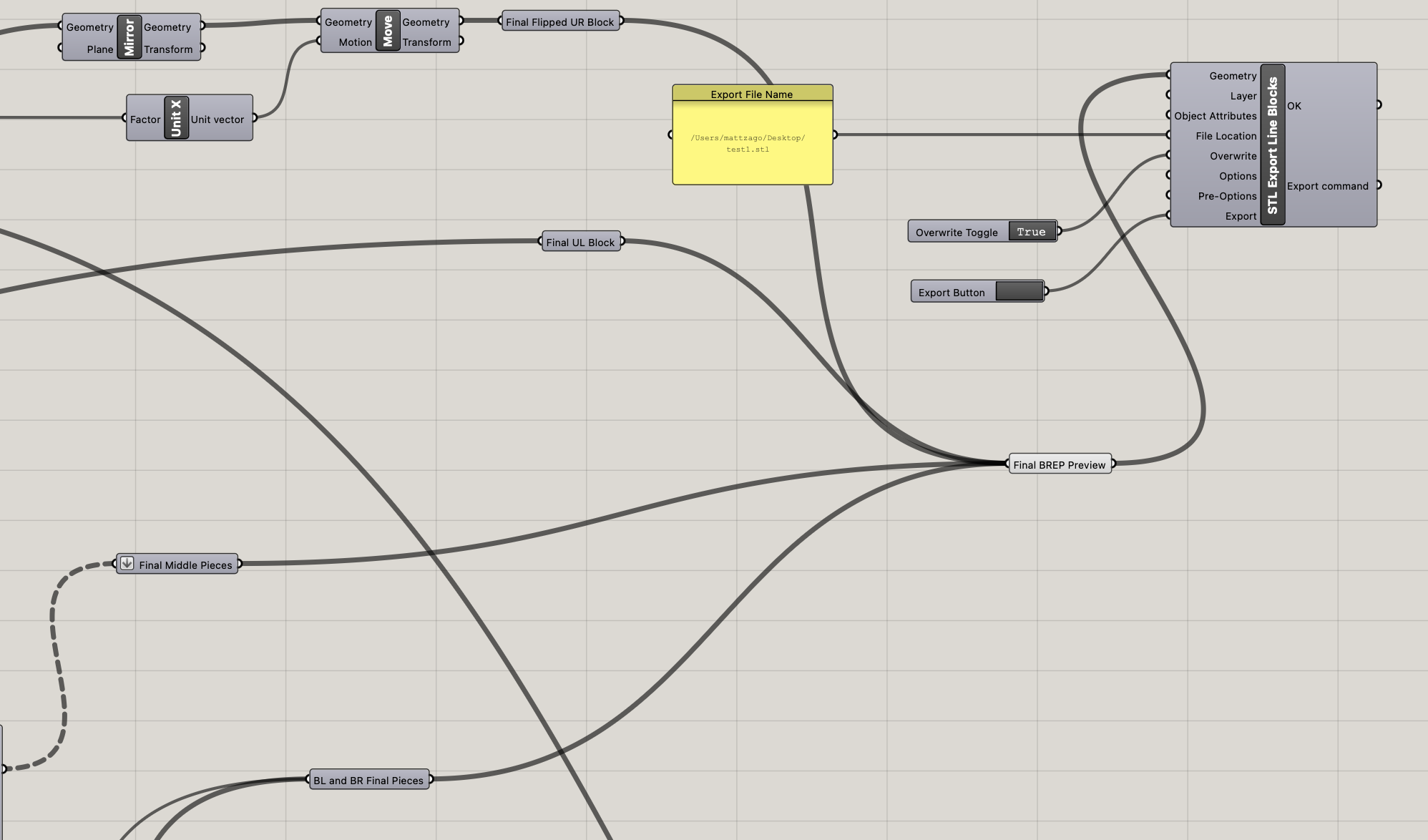
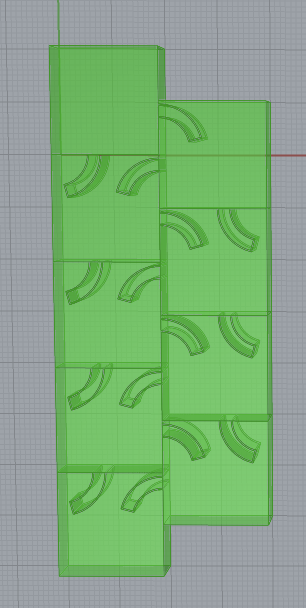
Here’s what the blocks for export look like in Rhino. The top two blocks being the upper right and upper left of the zipper and the bottom row being lower right and lower left.


Fabricating these blocks with Bambu Studio on my Bambu A1 Mini I ran into an initial issue where the first few layers wouldn’t stick. I just ended up using glue sticks, carefully cleaning my bed, and adjusting the first layer speed down to 25mm/s. Later prints went well and I just prototyped with 5-10% infills to make sure my blocks worked at all.


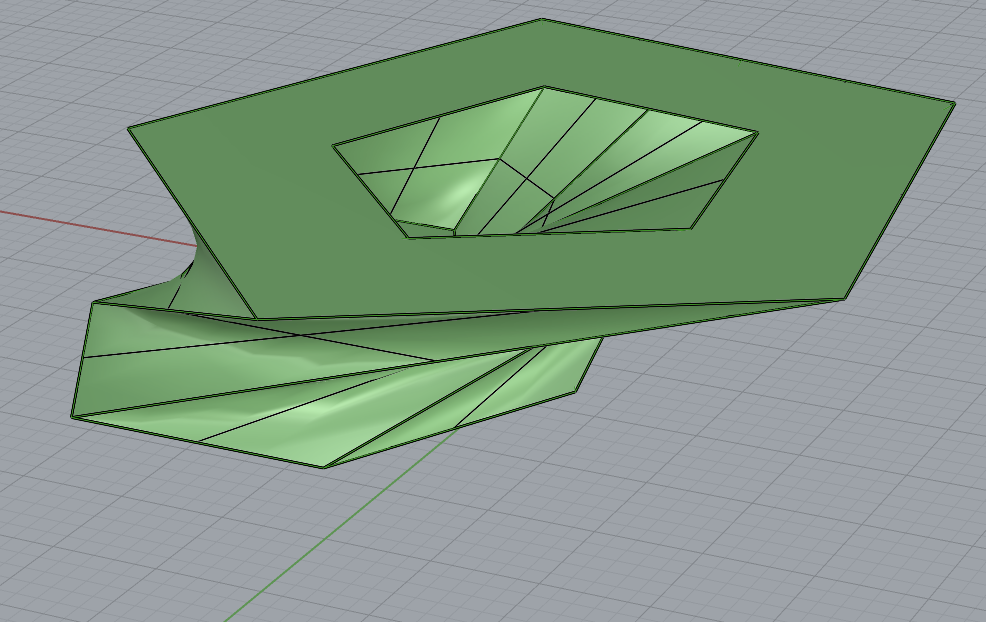
An early issue I noticed is that I hadn’t offset some of the teeth properly. You can see here where some of middle teeth don’t have the offset and while I could force the blocks to connect. It was easy enough to fix by checking that I was using the right breps making the middle blocks. Even with the missing offsets, thinner blocks could be connected into a long chain to make the zipper-like line.


With the fix for the offsets, I was able to print blocks that could be rotated into place to make the zipper-like structure.

Playing around with 0.25mm offsets I found things to be a bit too lose. In the z direction the blocks could be easily disconnected. 0.1-0.125mm had better results, but still at this point it was obvious that a better approach to lock the blocks in the z-axis was needed.

Just to check if in theory adding bottom/top layers that would lock the blocks in the third axis would work, I manually added top/bottoms in Rhino and made new versions. These new versions showed a few new problems. The blocks being printed without being rotated meant that the teeth were no longer on the bottom of the bed and would have overhang issues printing 90 degrees. I was able to use a lot of force to rotate the blocks in place and (covered in reflections) if given more time I would make new 3d templates that print the teeth on top and get blocks locked in all three axes. The paper authors ended up with teeth templates that would print the flat side on the bed and teeth on top.


Just to test what I could do with the Flow Component, a manual curve and my 2d blocks, I made some experimental components and printed out a curved block structure and it still would rotate in place. For the purposes of my project the 2d method is what I tested the most, but I was encouraged by the results of the curved version that deformed my teeth templates with curves. I think this could be adapted with flipping the printing, and adding top/bottom layers to lock the teeth in. This would result in actually getting close to the StructCurves in the research paper.


Reflection
I’m very appreciative that I narrowed the scope of my project a bit. Reading the research paper makes everything seem very simple, but through the fabrication process it became obvious how much nuance there is that I didn’t appreciate. There isn’t a significant discussion of simulation or optimization techniques in the paper, and I found through my own trial and error that getting anything that mimics a zipper-like line structure is possible. Simulating how this would work with complex curves and be rigid in the x,y, and z axes would take a significant amount more work compared to just adjusting where the teeth arcs are, changing the offset a bit, and reprinting over and over again.
With more time, I would completely recreate the process for creating the line of blocks to use Rhinoscript and python for the geometries with the same parameter usage for block size, teeth size, etc. This would significantly simplify how the grasshopper design would work.
I would make it so that the teeth offsets could be set for the sides independently from the tip because while I think in my setup a 0.125mm offset on each side is good, the offset on the tip of the tooth may need to be more to provide more space for the block to rotate. This would especially be true when the curve results in the teeth templates being more deformed. The newer design would allow a top/bottom value to be defined for the blocks that would seal in the tooth so that the blocks would lock into the joints and prevent movement in the z-axis.
I would also change things so that the printing would happen with the flat right/left sides of the block to be on the floor of the bed which would fix issues with extreme overhangs for printing the teeth.
Beyond that I would end up having to change the teeth layouts and try different curve layouts. A lot of test prints would then be done with different offsets and checking to see how much weight the new structures could bear.
If I got to the point where all that was working well, next up would be to try to find a nice way to either provide control points to the user to change for the curve layouts or a way to specify their own curves.
If all of that got to the point where it works, trying to automatically partition the blocks into multiple .stl file exports for multiple 3d printing bed layouts would be another step.
There’s a lot of work beyond that for trying to figure out ways to simulate the rotations of the teeth and prevent shapes that won’t align, etc.
Mid-Progress Milestone
Elevator Pitch
My goal is to design templates in Rhino/Grasshopper that create zipper-like line structures made of blocks that join together and become rigid. To get familiar with the joint tolerances the first templates will use “prismatic joints” and be rigid before and after being connected. The ultimate goal will be to design and print a flexible line structure that uses rotational joints to become rigid after assembly which was given the name of StructCurves by a recent paper presented at the “User Interface Software and Technology” conference in October 2024.
How Will Someone Use My Project
Using Rhino and Grasshopper someone can change values for the individual blocks like the width, length, height and joint teeth width and height. The initial testing will be with 4 block (2 left and 2 right) line structures, but I’m hoping I’ll get this to the point where you can define the length of an entire line structure along with the other parameters and correct number of pieces will programatically be generated. The final breps get baked and then manually exported in Rhino to .stl files which get sliced in whatever slicer happens to be used for 3d printing.
The current state of the project is that a template to generate four blocks using “prismatic” joints has been made and I’ve begun to print prototypes to figure out the tolerances needed for the joint teeth on a Bambu A1 mini with a 0.4mm nozzle.
The grasshopper code is very rudimentary with code using input parameters like the block width, height, and length, and joint teeth width and length. Components like Box 2pt, Solid Union, and Solid Difference, are used to add and subtract the teeth depending on the block. Moves are used to make sure the difference blocks aren’t connected so that when they’re baked and output, the slicer will correctly print individual blocks.



The examples given for pristmatic and revolute joints in the original StructCurves paper as a reference (the scribbling on the image is mine):

I’m printing using a Bambu A1 mini with BambuStudio as the slicer.
Next up is getting revolute joints working with four blocks. I also want to get the code refactored to use python script components to make it easy to loop for given line lengths. If I get that far, then I can start to try to figure out how to print curves using the rotational joints.
Large #3 - “Travel through Another Dimension”
Assignment Description
We went through playing around with Grasshopper + Python to make our own custom slicer and g-code generator for 3d printing. This is done by taking contours of a 3d model, slicing it and exploring infilling the contours with more lines.
All code is located in my github repo under L3-Basic3DPSlicer.
Part 1: Building A Slicer and G-code Generator for 3d Printing
Task 1: Create a Basic Slicer for 3d Printing
Coming from our last assignment, I didn’t find it too difficult to make our basic cylinder and move it to the build plate midpoint. At this point we’re all pretty comfortable with translating objects, extruding, etc.
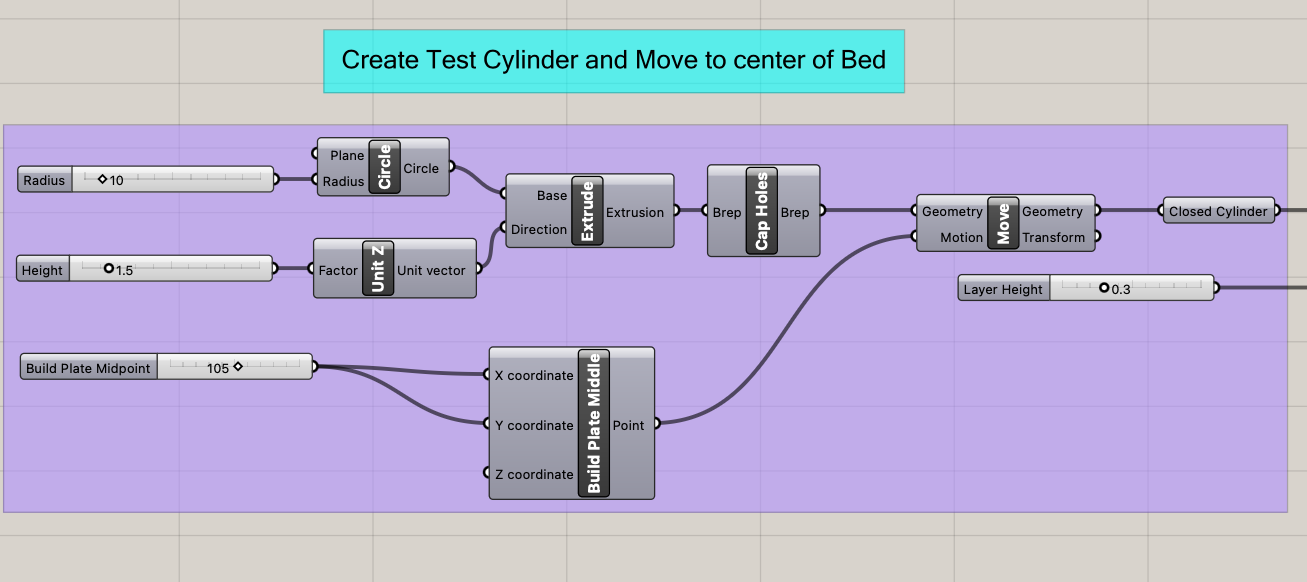
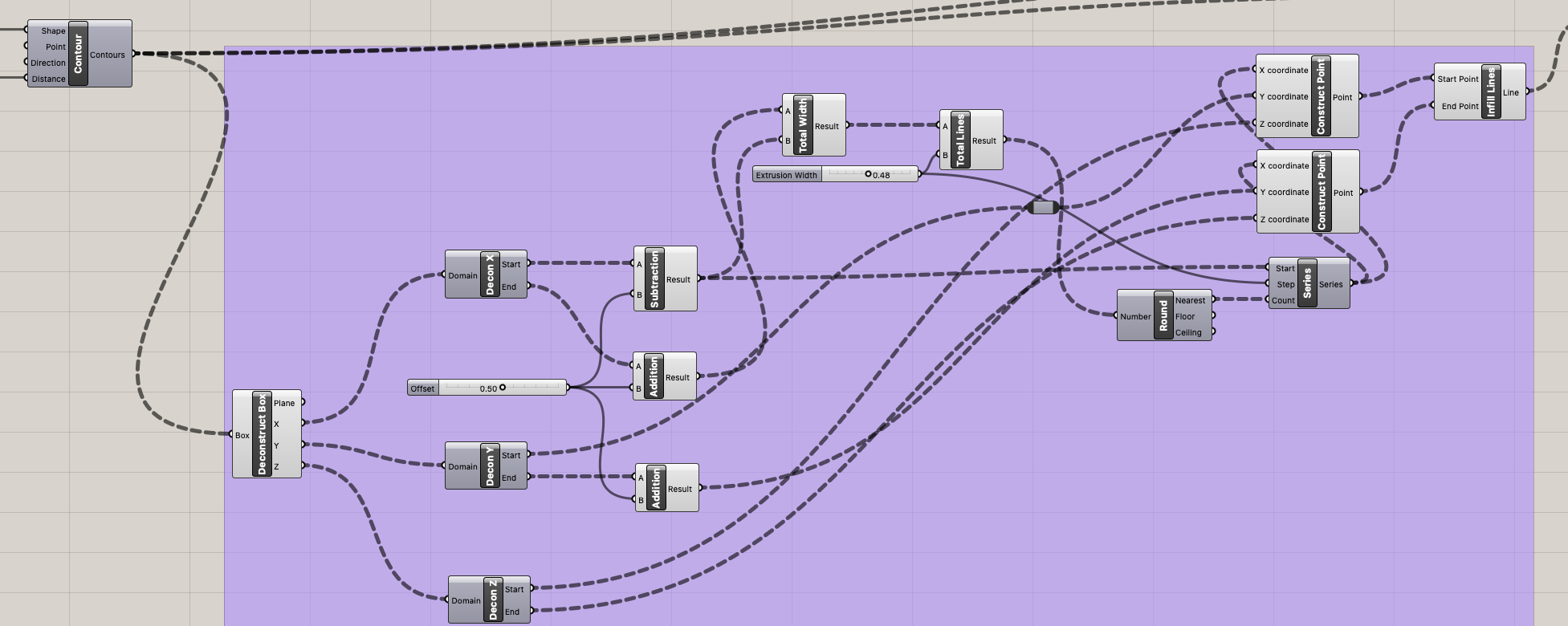
For constructing the infill lines, I went with an approach where I generated contours of my cylinder and then used deconstruct boundary box to get the domains of x,y,z for each contour and deconstructed those along with an offset to make the lines slightly larger than the perimeter. These new x,y,z values then got fed into a Series component with steps of the extrusion width to be used for points which finally got input into a line component to make lines. Finally the intersections of those lines and the original contours resulted in the infill lines.

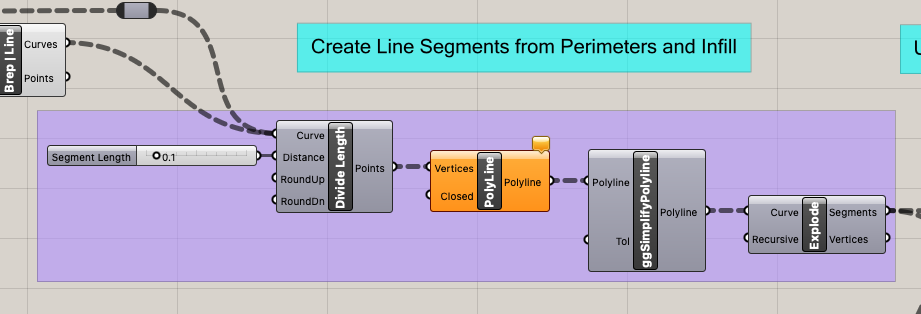
For making polylines, I didn’t have any problems following instructions to install the BullAnt plugin and get the ggSimplifyPolyLines component and then explode my polylines. The only thing I forgot was getting the perimeter lines back in the mix and had to make sure to connect my original perimiter contours to Divide Length.


Task 2: Create a G-Code Generator in Python/Graphics
Using the assignments template python code, I ended up with this resulting script.
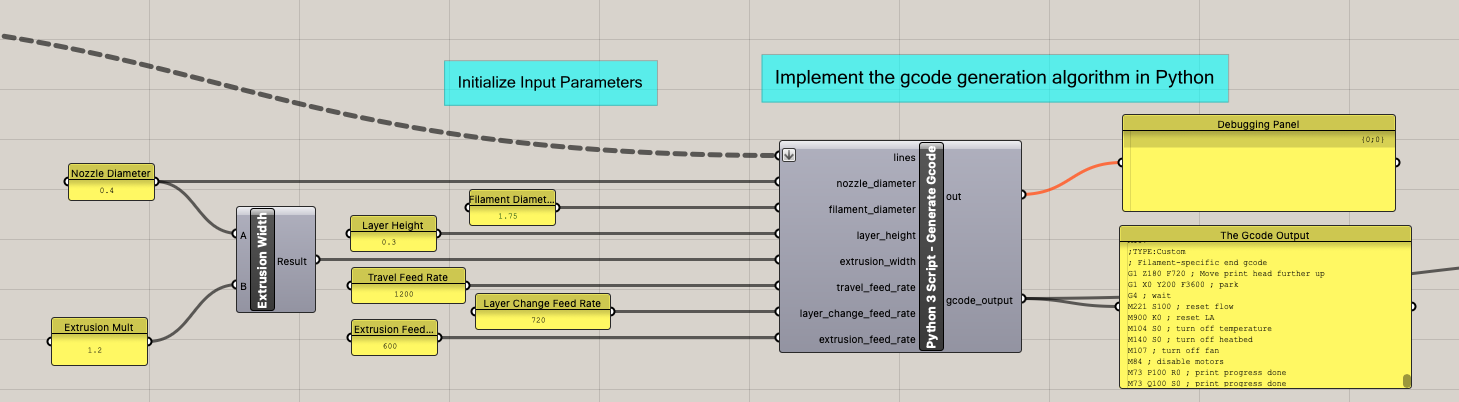
Working through the code, I did have to stop for a bit and review slides on how we calculate the E value. One thing I wasn’t sure on is that we always seem to assume we need to use z values to calculate 3d distance, but I see that our gcode doesn’t extrude via a move command with X, Y, and Z. The Z movements are supposed to happen with X/Y/Extrusion. I wonder if this is just a bit of future proofing or if there’s some crazy techniques with printing with a non-level bed.
I also didn’t realize that the python editor in Grasshopper has breakpoints and ended up using them a few times to figure out what I was doing wrong instead of using print statements everywhere.
For the algorithm for determining the extrusion value, I went back to slides and just started swapping in values from our Grasshopper file one by one and teased out the final result. It was straight forward taking it one step at a time.
Task 3: Exporting and Validating Your Generated G-code
Setting up the Pancake plug-in and getting a gcode file was straight forward.
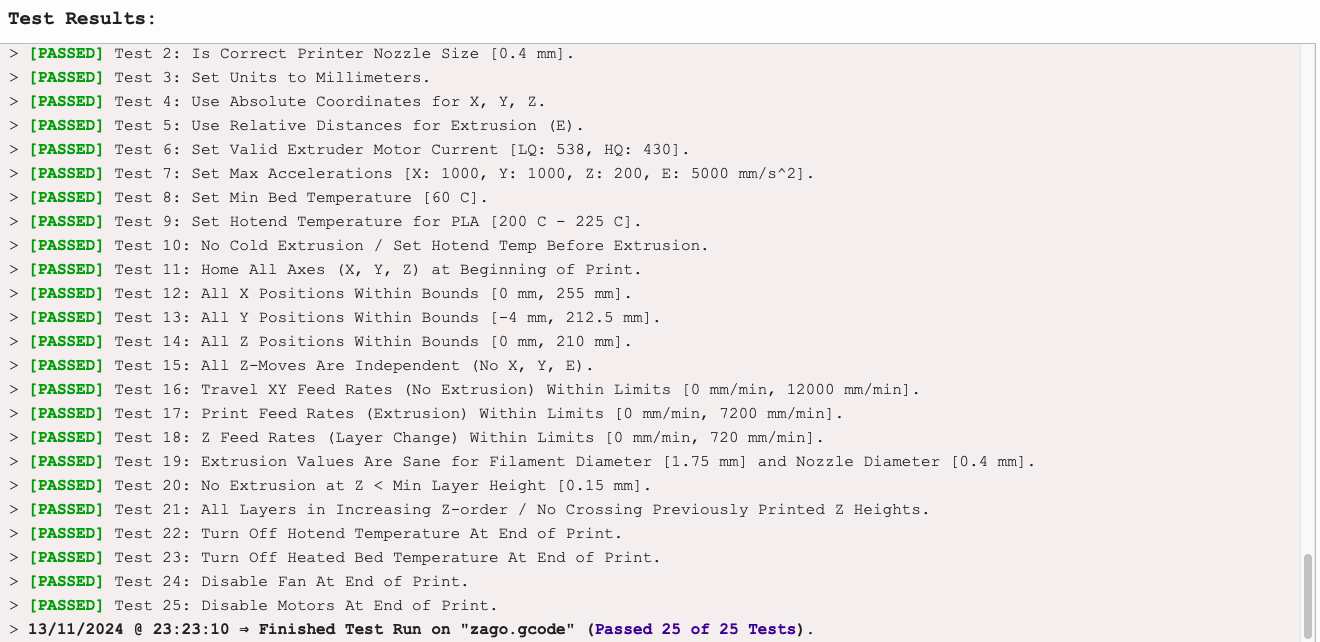
I was working back and forth with the gcode validator as I was fixing my script to extrude, etc. and I like a lot how Zupfe works with the easier sliders and simulated nozzle moving back and forth. I had a dumb mistake with an incorrect cylinder height set which caused the tester to fail. But after a correction I got 25/25 working tests.

Part 2: Printing Your Output and Comparing
Task 4: Fabricating Your G-Code and Comparing Slicers
I had to take some feedback from Part 1 and address some major issues with my gcode. While my gcode passed the tester, I didn’t pay close attention to instructions describing that the first layer would be 0.3mm and that a 1.5 height cylinder should have 5 total layers accordingly. I changed things by having the cylinder height subtract 0.3mm and have the move to the center of the build plate also offset the z height 0.3. This resulted in the correct 5 layers in my gcode where layer 1 is 0.3 and layer 5 is 1.5 with the layer heights being 0.3 making the total height 1.5.
Printing on the BTU MK3S+ printers had a small hiccup in that my large SD card (128GB) even formatted correctly would give a firmware error on the printer when I tried to print my gcode files. I used a smaller card and then my prints each completed in around 8 minutes. You can see the layer differences looking closely at each print in that the reference cylinder has more layers than our 5 layer version. Watching the extruder motion made it obvious that the reference cylinder was printing differently as well even though it had more layers. I looked in prusa slicer a bit more to confirm the differences and found the reference cylinder used 0.1mm layer heights for 14 layers and also had a more efficient serpentine path for the infill lines which eliminates a lot of wasted travel back and forth. The infills also rotate layer by layer which I can make a guess at might be more structurally sound compared to our version with aligned infills on every layer. The reference .stl also sliced with a brim around the cyclinder on the first layer.
For my cyclinder, I noticed some weirdness with the x/y movements on the first layer where some material was extruded before the cyclinder itself was extruded. Also some materials make a thing string (sorta like string cheese) when it moved up after the final layer. I didn’t do another test print to confirm if this behavior reproduced, but if I had more time I would probably do multiple prints and then determine if I had an issue with my gcode or if it was the printer itself.
For these images, the first is the reference cylinder and the second is my cylinder.


Mini #3 - “A Seat at the Table”
Assignment Description
This assignment was to get us comfy designing some parametric furniture in Grasshopper/Rhino and then get them 3d printed using standard .stl files on FDM/FFF 3d printers.
All code is located in my github repo under m3.
Task 1: Create Parametric Table or Chair Designs
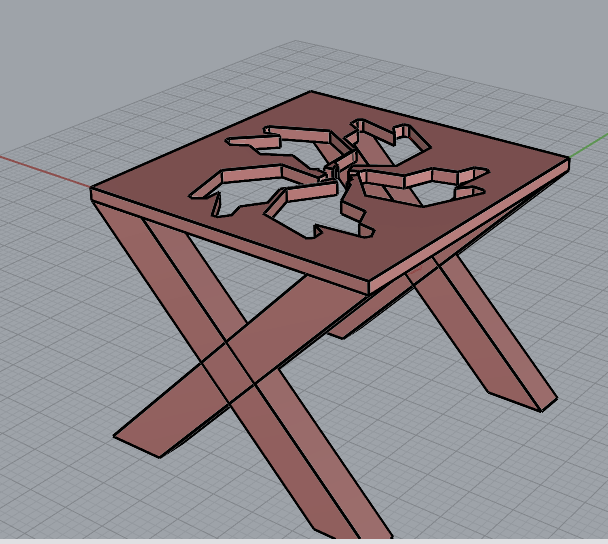
This would be the very first time I’ve ever 3d printed anything. I looked a bit into how I could design a table without needing support material and looking into how chamfers work and how to try to have a good enough angle for the legs to not have an overhang.
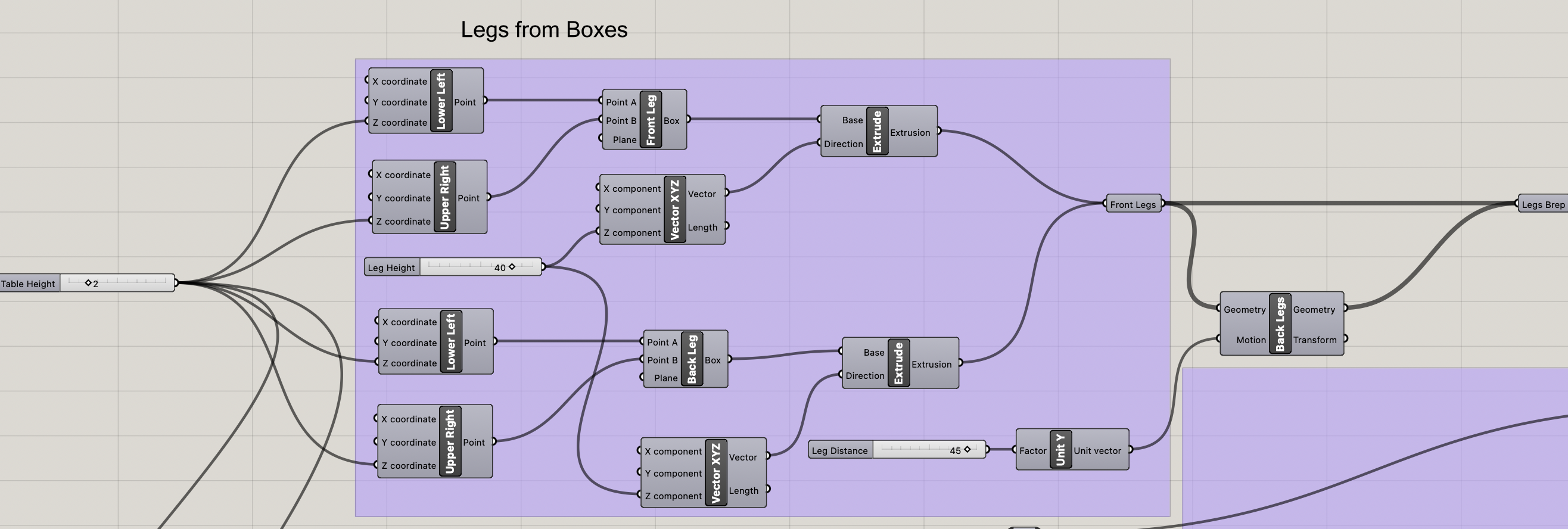
The result is that I ended up designing a cross leg table with the table top on the bottom of the plane (to make it easier to 3d print). I started with some simple 2d boxes that get extruded diagonally to become the legs. I used the move component to move the legs around to get the 4 total legs of the table.
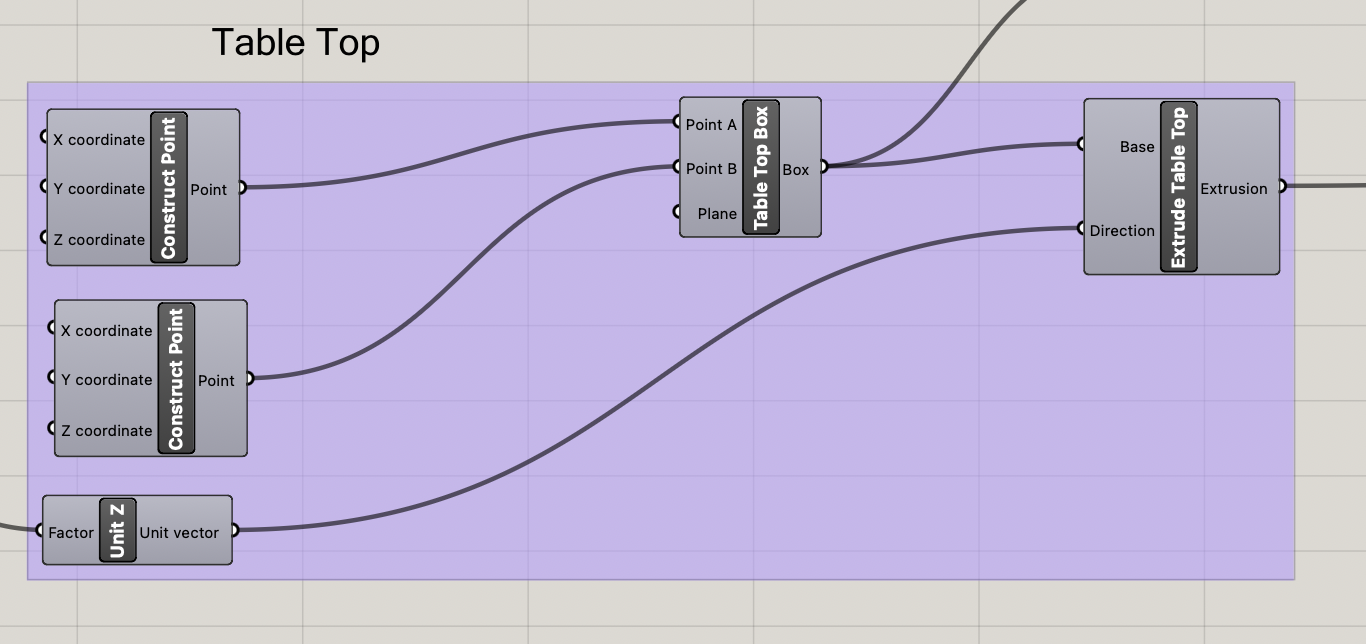
For the table top, I keep things simple and again use an extruded box.
 .
.
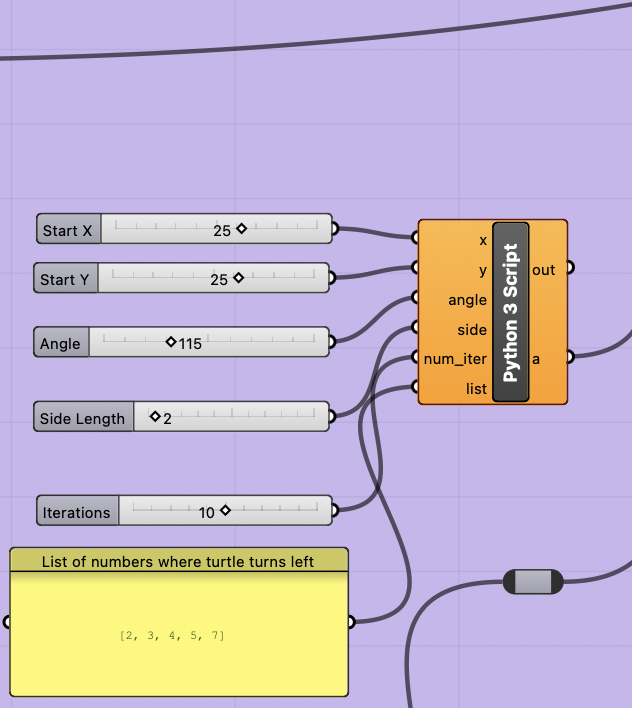
To make my design parametric, I decided to play around with the Python 3 script component to code up a rudimentary turtle class that is used to emulate the spirograph code from one of the classes recommended readings, Turtle Geometry: The Computer as a Medium for Exploring Mathematics.
The code is pretty simple. I create a very basic turtle class that supposed the basic forward, back, right, left, and pen_up/pen_down. The turtle class stores points in path which gets used to return polylines back to grasshopper of the spirograph.
A spirograph function runs through the given iterations and turns left for iterations that are in the input list and right otherwise. As mentioned, the points get stored in the turtle object which then finally gets output as a polyline.
Number sliders are used for basic things like iterations, angle, starting x/y, side length, and the list of iterations to turn left. Using panels to get strings is pretty easy in Grasshopper -> Python 3 script, so overall I was pretty happy with how simple it was.
"""Grasshopper Script"""
import rhinoscriptsyntax as rs
import math
import Rhino.Geometry as rg
"""A basic turtle class that assumes we're on the z=0 XY plane"""
class Turtle:
def __init__(self, x, y, angle):
self.x = x;
self.y = y;
self.angle = angle # in degrees
self.pen_down = True
self.path = []
self.path.append(rg.Point3d(self.x, self.y, 0))
def forward(self, distance):
x = self.x + distance * math.cos(math.radians(self.angle))
y = self.y + distance * math.sin(math.radians(self.angle))
if self.pen_down is True:
self.path.append(rg.Point3d(x, y, 0))
self.x = x
self.y = y
def back(self, distance):
# Just go forward the negative distance
self.forward(-distance)
def right(self, angle):
self.angle -= angle
def left(self, angle):
self.angle += angle
def pen_up(self):
self.pen_down = False
def pendown(self):
self.pen_down = True
self.path.append(rg.Point3d(self.x, self.y, 0))
def get_polyline(self):
return rg.Polyline(self.path)
# Gspiro technique adapted from Turtle Geometry: The Computer as a Medium for Exploring Mathematics pg. 38
def gspiro(turtle, side, angle, max_iterations, turn_list):
""" Main gspiro routine """
for _ in range(max_iterations):
subgspiro(turtle, side, angle, max_iterations, turn_list)
def subgspiro(turtle, side, angle, max_iterations, turns_list):
""" Subroutine that runs """
for n in range(1, max_iterations):
turtle.forward(side * n)
if n in turn_list:
turtle.left(angle)
else:
turtle.right(angle)
# Parse our input list into a new list
string_list = list
print(string_list)
string_elements = string_list.strip("[]").split(", ")
turn_list = [int(e) for e in string_elements]
iterations = int(num_iter)
# Run through our turtle script using our inputs for where the start should be
turtle = Turtle(x, y, 0) # Start at input given for x/y on the xy plane
gspiro(turtle, side, angle, iterations, turn_list)
# Output the polylines generated
a = turtle.get_polyline()
Back in Grasshopper I convert the polylines to surface and extrude it to be the same height as the table top so we can get a cutout effect (acrylic is going to be put on top so the table doesn’t have any holes).
A tricky thing I hadn’t thought of was how to make sure the spirograph gets aligned to the center of the table top. I ended up playing around with boundary boxes for the spirograph and then using the centroid of that and the table top to move the spirograph to the center of the table top.
The table top and the spirograph then get run through solid difference to make it so the spirograph is cut out of the table top and the final brep is generated.
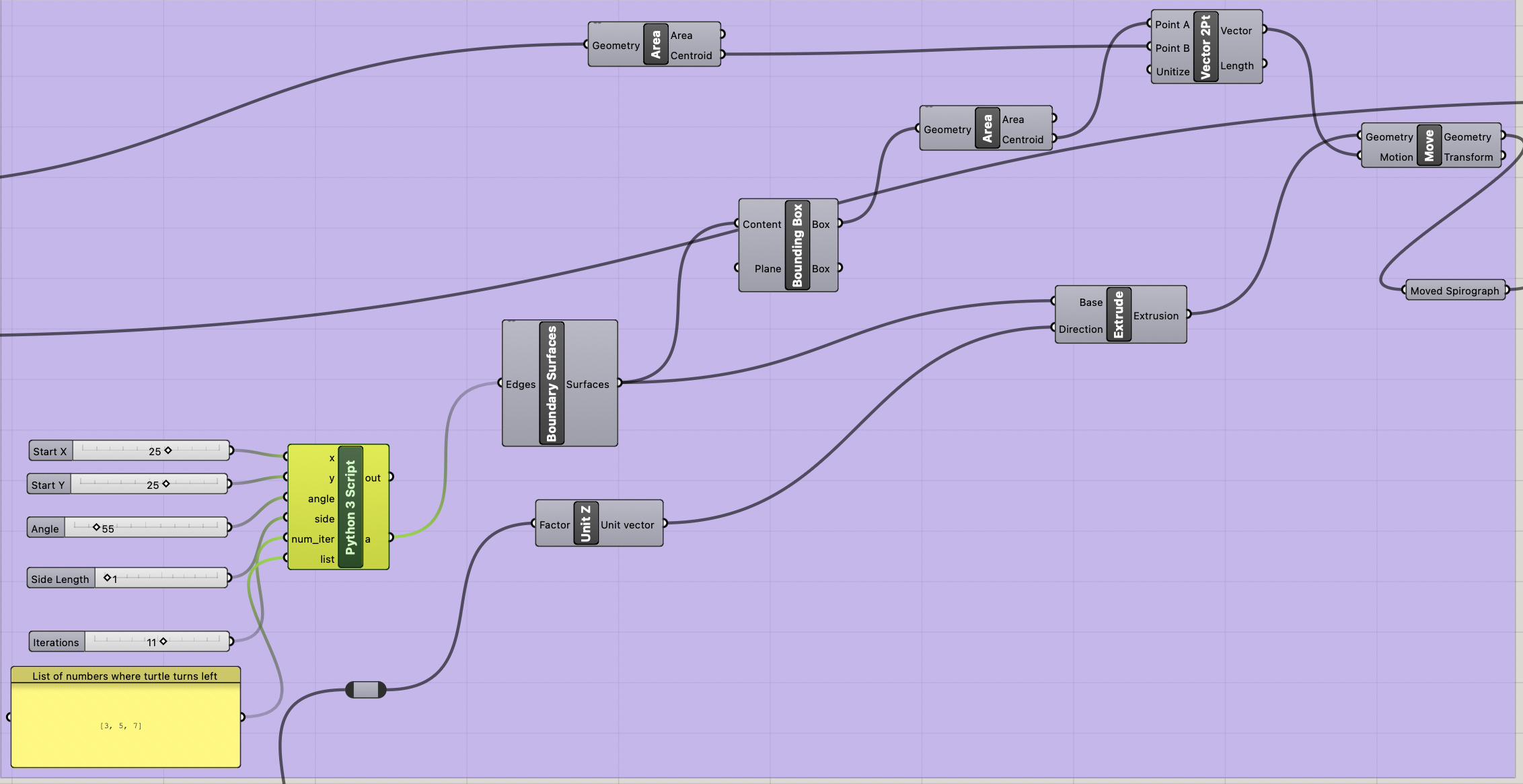
Here are the parameters and resulting models for 3 different designs.
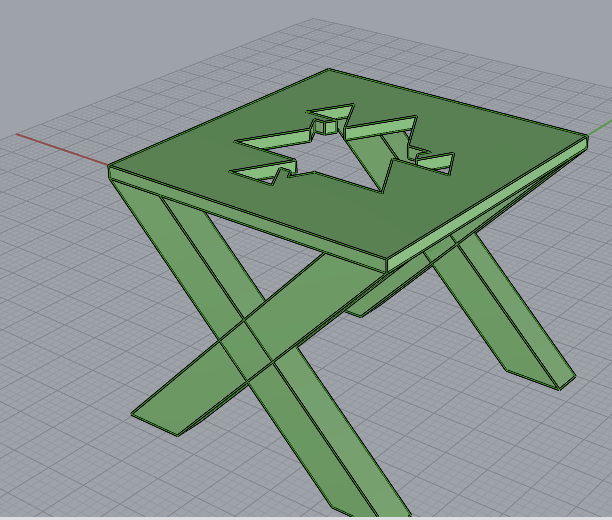

Task 2: Fabricate Your Designs with 3d Printing
Tempting fate, I decided to print two of my designs at the ITL a few hours before this assignment is due. ITL uses a weird cloud slicing program instead of Prusa Slicer, but I had already tried using my .stl files in Prusa Slicer with different parameters to get a feel for long they would print on a Prusa MK4. I knew from my design that I wouldn’t need support materials and went ahead and queue up my prints. The exporting of my .stl files was just a matter of baking my final brep, selecting the entire baked model in Rhino and exporting to .stl. I didn’t find I had to do a SolidUnion step since my brep already had all the geometry.
For the table tops, I laser cut some simple acrylic squares. My first print of a table went fine. It took about an hour to print on normal quality which makes sense given my design is very small (about 40m x 40mm x 50mm).




The second print also printed in about an hour of time without any issues. Both models had 15% infill.
If I spent a bit more time of this assignment I would probably tweak my grasshopper code to make a repeating pattern for the spirographs and grid layout it across the table top for more interesting visual patterns.
I’m overall happy that things printed in a reasonable time frame without any major problems. I’ve never actually 3d printed anything before so this was a good excuse to learn some basics about designing objects for slicing and getting out some basic prints.
Large #2 - “Stacking Up”
Assignment Description
Figure out how to fight with Grasshopper and Rhino to generate parametric designs and fabricate them using laser cutting. The designs will go from 3d to 2d with slices. The laser cut slices will get assembled and glued to make them 3d again.
All code is located in my github repo under l2. It’s grasshoper xml code that should properly load.
Task 1: Parametric 3d Designs
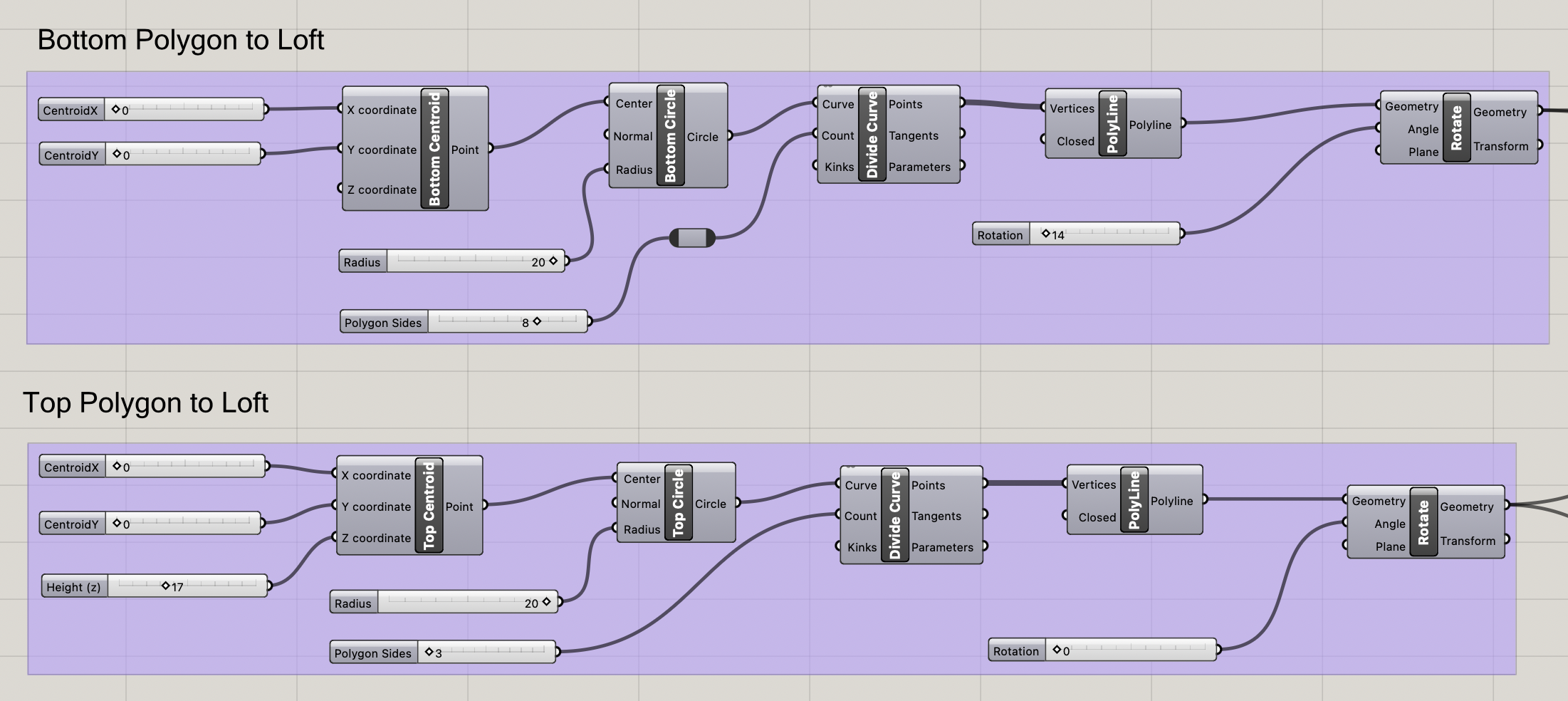
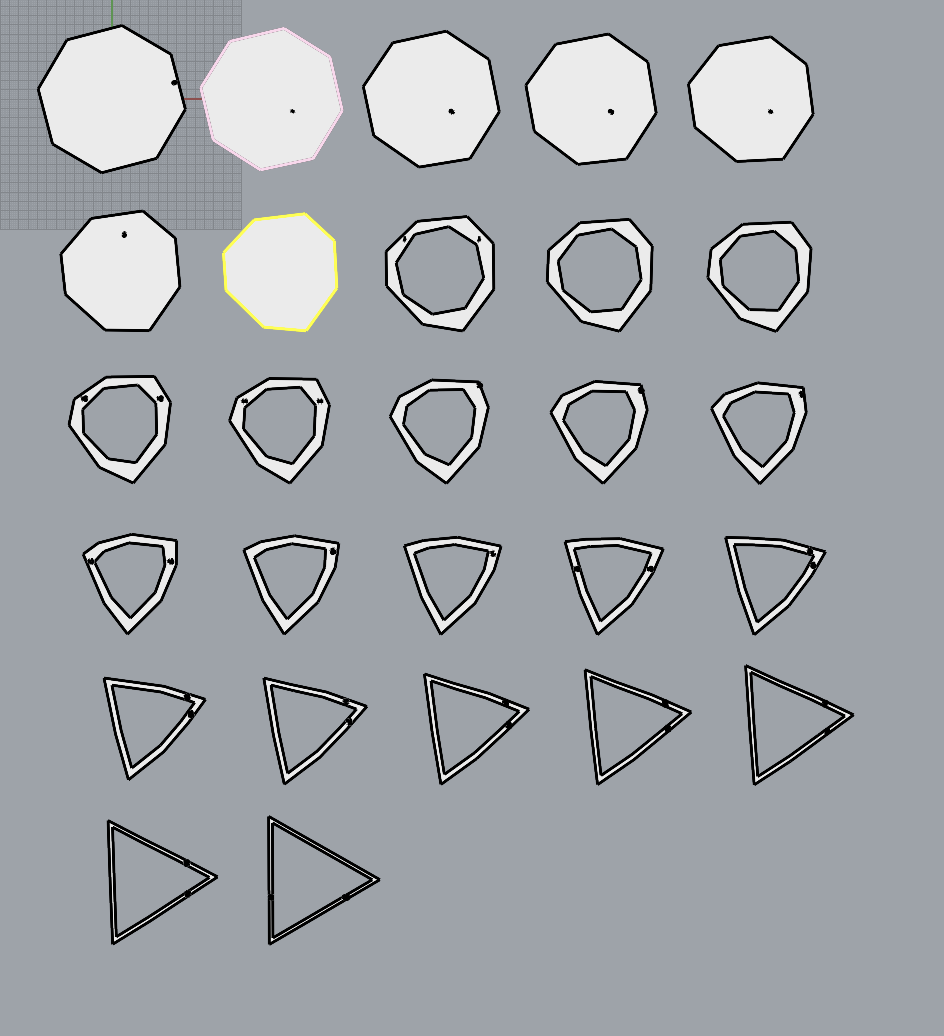
I decided to create a design where Grasshopper creates a “top” and “bottom” regular polygon and lofts between them. To make it a little more interesting I decided to carve out an inset as well to make the design hollow. The polygon is created by first making a x,y,z coordinate for the centroid and making a circle. The circle is then divided into curves and converted into polylines based on the number of sides. Finally an angle rotation is possible to create more interesting designs.
The ways to change the top and bottom are:
-
Centroid X,Y Coordinates: Changing where the centroid is (the default is 0,0,0). This can create exaggerated tilting effects if the top and bottom centroids are not aligned.
-
Radius: The radius can be changed so that the either top or bottom can be larger or smaller for different effects.
-
Number of polygon sides: The slider can be changed from 3-10 to create different regular polygon shapes.
-
Angle Rotation: The polygons can be rotated to create various twisting effects from the lofting. This is quite tricky to tweak to get the best effects because lofting two different polygons will naturally have some twisting already.
-
Height: For the top, the height can be changed to modify the total height of the design.
Ways to change the inset include:
-
Inset hole height: This creates the base where there is no inset. Taking into account slice heights when we later slice is important.
-
Top/Bottom inset distance: This creates the inner lofted shape. Slight negative values (-1, -2, etc.) tend to work best, but viewing how things look in Rhino is very important.

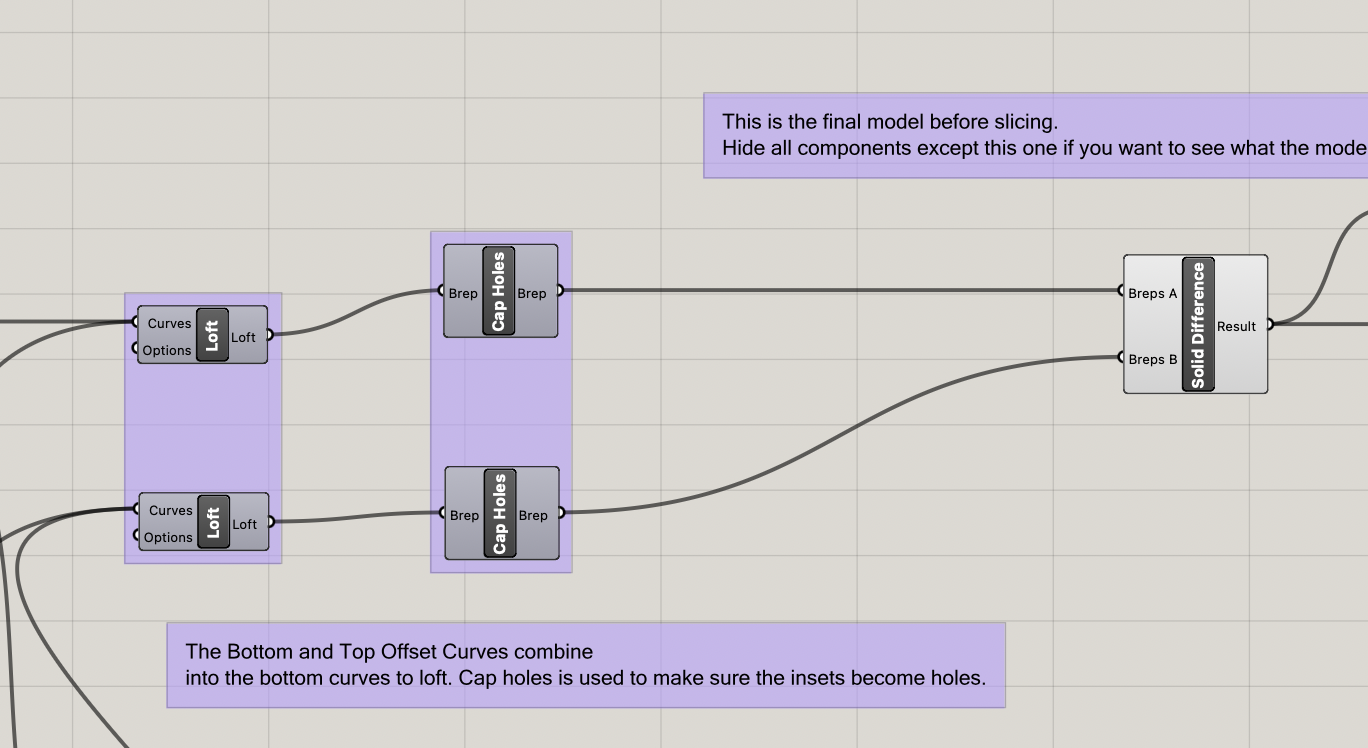
Once we have all the curves for the top and bottom polygons and insets, we loft each and use cap holes to make sure the top and bottom get added besides the lofted shape. Finally solid difference is used to subtract the inset to create the hollow inside (if inset is used).
Here are five examples generated from these grasshopper components.



Task 2: Creating a 3D-to-2D Slicer
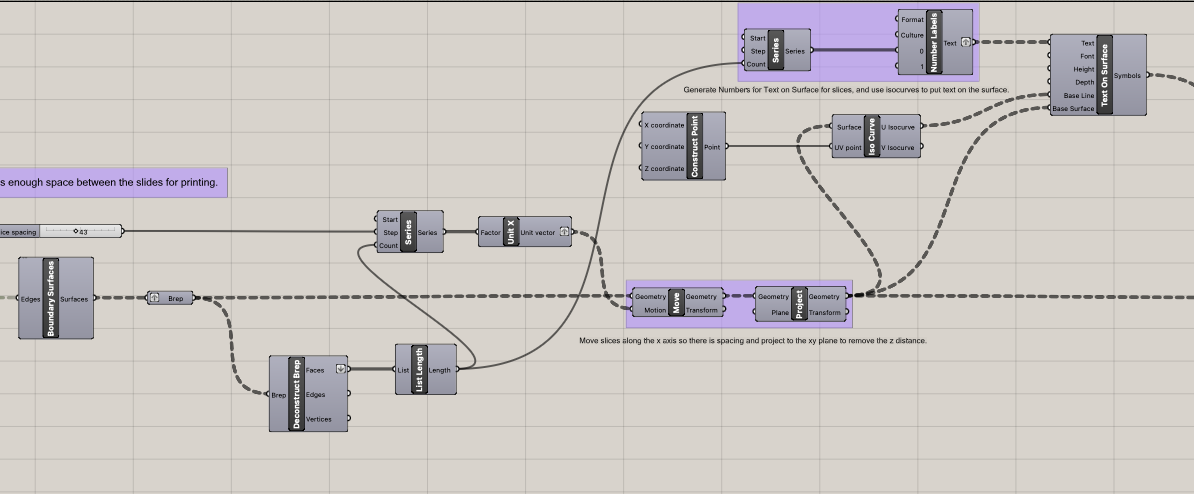
For creating slices, I took my designs from task 1 and deconstructed the brep to be fed into a Contour component along with direction vector of 0,0,1 (z-axis). This creates the initial slices. The slice height is also changable (for my cardboard 4 = 4mm is the right height)
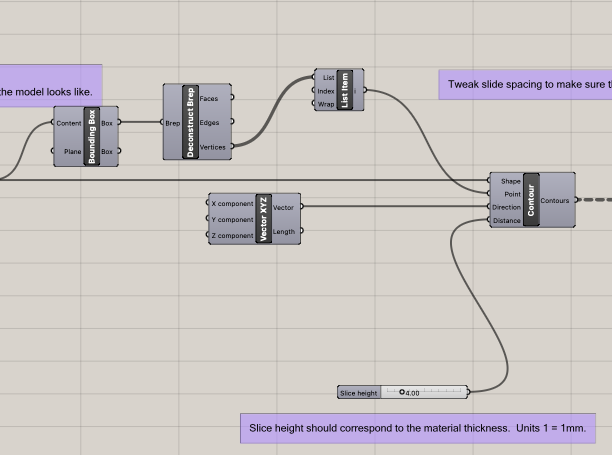
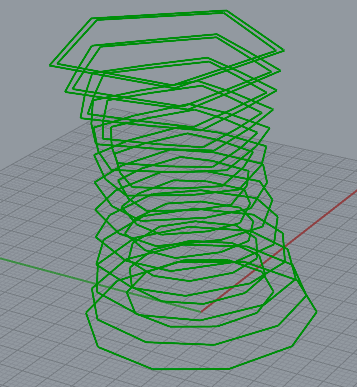
Then the slices get moved horizontally with slice spacing slider that you can tweak to make sure there’s enough distance between the slices. Those slices get projected to the xy plane so that they’re no longer staggered along the z-axis.
Text on surface is used along with formatted text of {0} for the number of slices to etch the slice number starting from 0 on to the slice. I used iso curves as the base line input to text on surface because it puts the label in a better place when the slices get narrower with the inset cut out. Otherwise the label could be on a part of the slice that is cut away.
An examples designs baked in Rhino and another exported from rhino and re-aligned for laser cutting.

Task 3: Exporting and Fabricating Your Design
I decided to fabricate at CU’s ITL laser printers and that meant working with Corel Draw to print my designs. A few things became apparent after fabricating a few different designs. I would bake my final shapes, toss them into Corel Draw, and then laser cut.
-
The spare cardboard I had was not quite 1/8th an inch. I ended up using calipers to measure the cardboard and find it was 4mm. This made me change my grasshopper values to reflect 4 being the slice height. My first print outs were distorted because I didn’t do the math correctly for slice heights.
-
Cardboard tends to flap around compared to acrylic. I used some spare cardboard to weigh it down, but I didn’t realize the cardboard would move so much during printing.
-
The smell of burnt cardboard is pleasant to me.
-
Children’s washable elmers glue sticks are terrible compared to plain old elmer’s glue.
-
My initial designs would cut the slicer number label into the slice. This works great until you end up with very thin edges to my designs with insets. With the kerf from the laser and a very narrow cut, the number ends up cutting through the entire side. If I spent more time on my design. I tried out a different strategy for a later design by baking just the text on surface layer and the shapes seperately. Then I lined them both up in corel draw and made the numbers raster to be engraved instead of cut. This did work, but the engraving was a little bit too light compared to the cuts. I would need to play around a bit more with the engraving settings on the laser cutter to get darker numbers.
-
Alignment is a huge problem with gluing the layers. I generally just tried to align manually by looking at my slices and glueing appropriately, but that’s really error prone. A classmate mentioned etching a + at the center of their slices to help with alignment, and I do think this would work. I can’t make it in the center, but I could engrave a plus or other lines across the layers to make it easier to glue together, or even a tiny notch for ever faster alignment.




Large #1 - “Stringing Along” - Thursday, October 3, 2024
Assignment Description
Learn what L-Systems are and get comfortable using procedures and algorithms with Processing to create some interesting designs. A subset of those designs will be laser cut. As a bonus, maybe play around with a probablistic approach to make more random (not deterministic) designs.
All code is located in my github repo.
Task 1: Using Turtle in Processing
All code for task 1 is in my github repo.
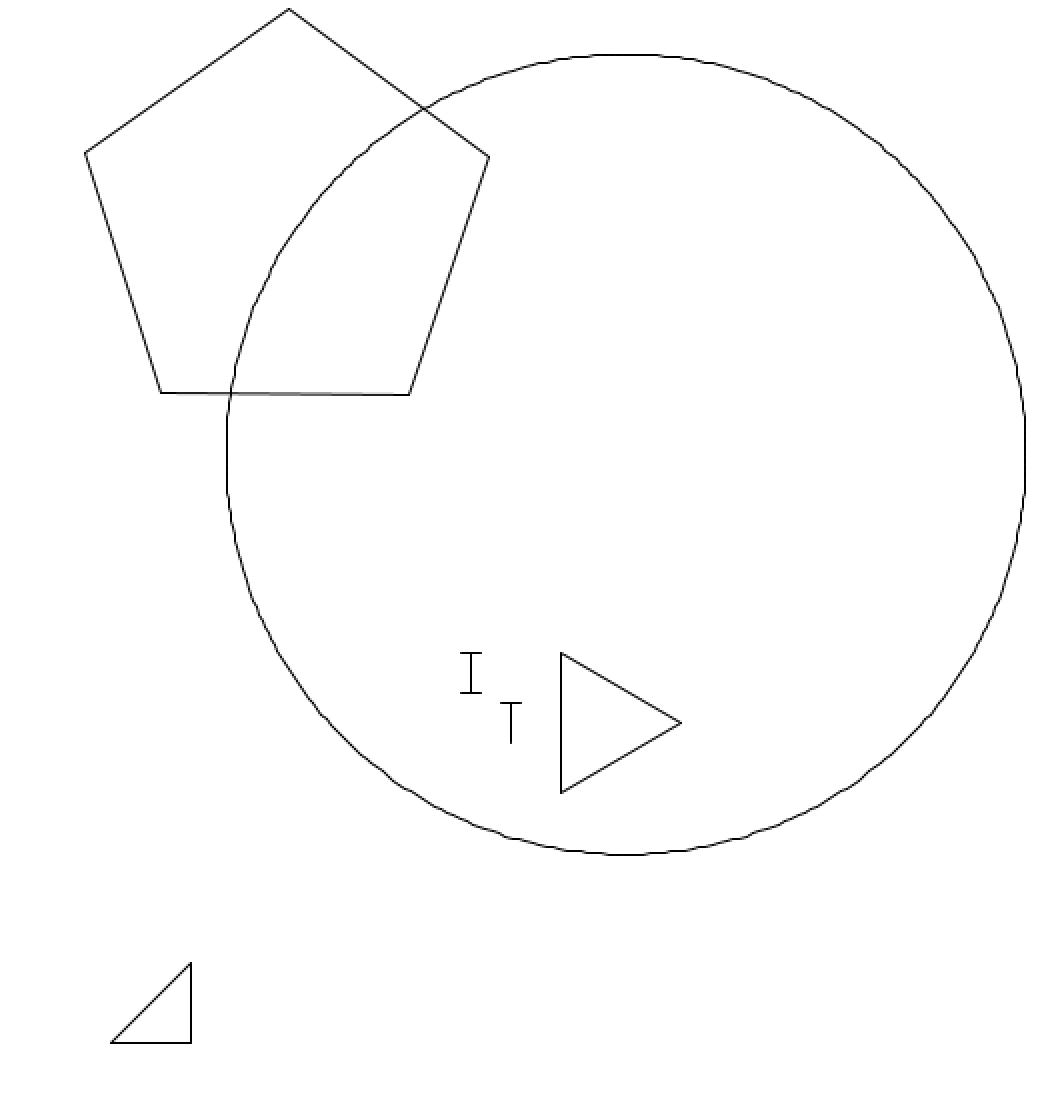
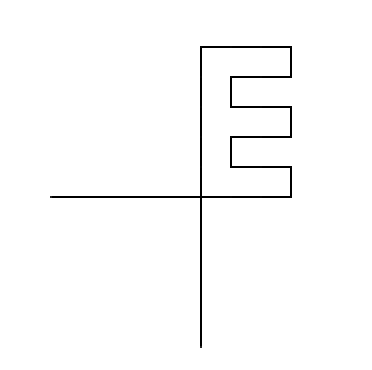
This task wasn’t too much trouble. It involved getting used to using the Turtle library in Processing to make some basic letters and shapes. Specifically we were tasked with creating these:
- Capital I and T
- A triangle
- A regular pentagon
- A circle with a well defined radius
It became obvious pretty quick that if you want to run a lot of different drawing functions, you’ll want a utility function to easily set/reset the turtle x/y and heading via setX() and setY() and setHeading(). I just ended up calling this setXY()
For drawing a triangle, you start to think back about the different types of triangles (right triangle, equilateral, etc.). I initially drew a equilateral triangle via code like this.
// Basic utility function for quickly setting the x/y and the rotation
void setXY(float x, float y, float rotation) {
t.setX(x);
t.setY(y);
t.setHeading(rotation);
}
But the assignment asks for a regular pentagon, and working through the regular pentagon code, you can quickly realize you can generalize any regular polygon by just knowing the side length and number of sides after working through calculating the internal angle given the number of sides. I then ended up with a more general draw function for any regular polygon:
// Draw a regular polygon (all sides are same length and all internal angles are the same
// at a given x,y with length s for the sides and n for the number of sides, and a rotation
void drawRegPoly(Turtle t, float x, float y, float s, int n, float rotation) {
setXY(x,y, rotation);
float angle = 180 - ((((float)n - 2) / n) * 180);
for (int i = 0; i < n; i++) {
t.forward(s);
t.right(angle);
}
}
Drawing an equilateral triangle is just the specific case of drawRegPoly with 3 sides. I ended up working up the right triangle as well which is just the case of using the Pythagorean theorem for the hypotenuse calculation and making sure the internal angles are 45, 45 and 90.
// Draw a right triangle given x,y with the two shorter side lengths and the given rotation
void drawRightTriangle(Turtle t, float x, float y, float s, float rotation) {
float h = sqrt(pow(s,2) + pow(s,2));
setXY(x, y, rotation);
t.right(45);
t.forward(h);
t.right(135);
t.forward(s);
t.right(90);
t.forward(s);
}
For a “well-defined” radius triangle. That made me assume that we need to be able to draw a circle with a given radius and not just any arbitrary one. Turtle Geometry: The Computer as a Medium for Exploring Mathematics already explained how to do an arbitrary one where you rotate just 1 degree and move forward 1 degree. But for doing a circle with a defined radius we can use the circumference formula of a circle and calculate the amount to move for each iteration. With enough iterations the line segments connected look like a circle (zooming in would show that isn’t truley the case), but at this point the approximation is enough.
// Draw a circle at a given x,y with a given radius
void drawCircle(Turtle t, float x, float y, float r) {
setXY(x, y, 0);
// Use circumference to allow us to draw any radius
float c = 2 * PI * r;
float step = c / 360;
for (int i = 0; i < 360; i++) {
t.forward(step);
t.right(1);
}
}
Task 2: Implement the L-System Framework
All code for task 2 is in my github repo.
The boilerplate code provided for the compfab class was pretty complete. I’ve dabbled into Java every few years for software products I couldn’t avoid it (Tomcat backed web apps and building on Java with Scala for example). One quirk I was curious about was how to process complex multi-tokens. For example if we had F+A -> FF+AA, but I avoided that for this course work to go with simplier iterations parsing each current string character by character for swaps.
I didn’t find the overall coding to all that bad for getting the sample l-system working, but it’s obvious just playing around that you tend to get exponent increases in elements in the l-system as you go up in iterations because of how slowly the computation + draw steps are for iteration 3+.
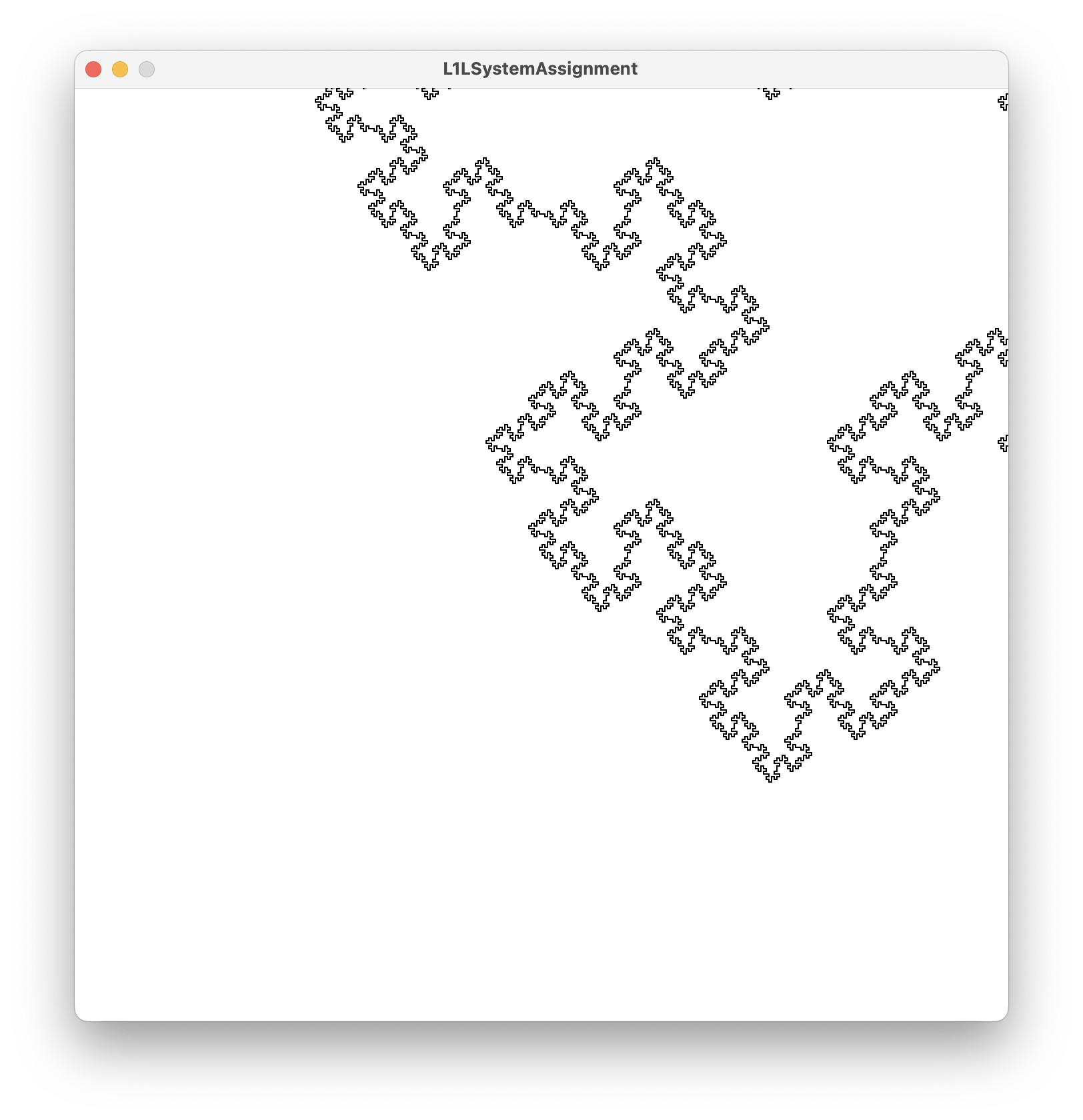
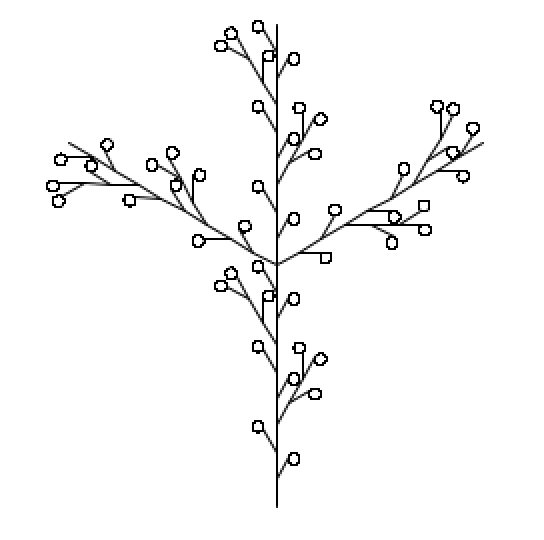
Task 3: Create 3 Unique L-System Designs
All code for task 3 is in my github repo.
It was fun to play around with different designs. I initially started with trying to think about grid-like designs with 90 degree angles. This required thinking about the starting and finishing points to try to make sure the rule substitutions would create an expanding design.
The code for designs A,B, and C are in the initA(), initB(), and initC() methods of my ExampleLSystemDesigns.pde.
| Design A | |
| Vocabulary | “F”, “A”, “+”, “-“ |
| -> Variables | “F”, “A” |
| -> Constants | ”+”, “-“ |
| Rules | (“F” -> “AFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFA”) |
| (“A” -> “FFFFFFFF”) | |
| Axiom | “F” |
| Move Distance | 30 |
| Angle | 45 |
| Scale Factor | 1 |
| Drawing | “F” means move forward move distance |
| “A” means move forward move distance * 5 | |
| ”+” means turn right by angle | |
| ”-“ means turn left by angle |
Iterations from n=0 to n=3


| Iteration (n) | Iteration String |
| 0 | F |
| 1 | AFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFA |
| 2 | FFFFFFFFAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFA++AFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFA++AFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFA++AFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFA–AFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFA–AFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFA++AFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFA++AFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFA–AFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFA–AFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFA++AFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFA++AFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAFFFFFFFF |
| 3 | AFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAFFFFFFFFAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFA++AFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFA++AFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFA++AFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFA–AFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFA–AFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFA++AFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFA++AFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFA–AFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFA–AFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFA++AFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFA++AFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAFFFFFFFFFFFFFFFFAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFA++AFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFA++AFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFA++AFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFA–AFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFA–AFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFA++AFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFA++AFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFA–AFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFA–AFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFA++AFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFA++AFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAFFFFFFFFFFFFFFFFAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFA++AFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFA++AFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFA++AFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFA–AFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFA–AFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFA++AFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFA++AFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFA–AFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFA–AFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFA++AFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFA++AFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAFFFFFFFFFFFFFFFFAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFA++AFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFA++AFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFA++AFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFA–AFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFA–AFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFA++AFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFA++AFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFA–AFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFA–AFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFA++AFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFA++AFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAFFFFFFFFFFFFFFFFAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFA++AFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFA++AFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFA++AFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFA–AFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFA–AFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFA++AFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFA++AFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFA–AFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFA–AFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFA++AFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFA++AFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAFFFFFFFF++FFFFFFFFAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFA++AFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFA++AFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFA++AFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFA–AFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFA–AFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFA++AFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFA++AFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFA–AFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFA–AFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFA++AFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFA++AFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAFFFFFFFFFFFFFFFFAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFA++AFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFA++AFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFA++AFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFA–AFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFA–AFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFA++AFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFA++AFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFA–AFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFA–AFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFA++AFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFA++AFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAFFFFFFFFFFFFFFFFAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFA++AFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFA++AFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFA++AFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFA–AFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFA–AFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFA++AFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFA++AFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFA–AFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFA–AFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFA++AFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFA++AFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAFFFFFFFF++FFFFFFFFAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFA++AFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFA++AFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFA++AFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFA–AFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFA–AFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFA++AFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFA++AFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFA–AFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFA–AFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFA++AFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFA++AFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAFFFFFFFF++FFFFFFFFAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFA++AFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFA++AFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFA++AFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFA–AFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFA–AFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFA++AFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFA++AFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFA–AFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFA–AFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFA++AFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFA++AFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAFFFFFFFFFFFFFFFFAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFA++AFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFA++AFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFA++AFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFA–AFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFA–AFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFA++AFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFA++AFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFA–AFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFA–AFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFA++AFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFA++AFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAFFFFFFFF–FFFFFFFFAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFA++AFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFA++AFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFA++AFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFA–AFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFA–AFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFA++AFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFA++AFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFA–AFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFA–AFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFA++AFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFA++AFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAFFFFFFFF–FFFFFFFFAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFA++AFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFA++AFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFA++AFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFA–AFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFA–AFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFA++AFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFA++AFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFA–AFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFA–AFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFA++AFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFA++AFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAFFFFFFFFFFFFFFFFAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFA++AFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFA++AFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFA++AFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFA–AFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFA–AFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFA++AFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFA++AFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFA–AFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFA–AFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFA++AFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFA++AFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAFFFFFFFF++FFFFFFFFAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFA++AFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFA++AFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFA++AFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFA–AFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFA–AFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFA++AFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFA++AFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFA–AFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFA–AFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFA++AFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFA++AFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAFFFFFFFF++FFFFFFFFAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFA++AFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFA++AFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFA++AFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFA–AFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFA–AFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFA++AFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFA++AFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFA–AFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFA–AFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFA++AFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFA++AFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAFFFFFFFFFFFFFFFFAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFA++AFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFA++AFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFA++AFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFA–AFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFA–AFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFA++AFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFA++AFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFA–AFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFA–AFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFA++AFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFA++AFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAFFFFFFFF–FFFFFFFFAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFA++AFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFA++AFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFA++AFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFA–AFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFA–AFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFA++AFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFA++AFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFA–AFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFA–AFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFA++AFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFA++AFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAFFFFFFFF–FFFFFFFFAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFA++AFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFA++AFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFA++AFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFA–AFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFA–AFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFA++AFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFA++AFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFA–AFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFA–AFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFA++AFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFA++AFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAFFFFFFFFFFFFFFFFAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFA++AFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFA++AFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFA++AFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFA–AFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFA–AFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFA++AFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFA++AFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFA–AFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFA–AFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFA++AFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFA++AFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAFFFFFFFF++FFFFFFFFAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFA++AFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFA++AFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFA++AFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFA–AFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFA–AFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFA++AFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFA++AFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFA–AFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFA–AFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFA++AFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFA++AFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAFFFFFFFF++FFFFFFFFAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFA++AFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFA++AFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFA++AFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFA–AFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFA–AFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFA++AFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFA++AFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFA–AFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFA–AFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFA++AFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFA++AFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAFFFFFFFFFFFFFFFFAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFA++AFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFA++AFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFA++AFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFA–AFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFA–AFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFA++AFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFA++AFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFA–AFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFA–AFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFA++AFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFA++AFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAFFFFFFFFFFFFFFFFAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFA++AFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFA++AFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFA++AFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFA–AFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFA–AFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFA++AFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFA++AFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFA–AFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFA–AFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFA++AFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFA++AFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAFFFFFFFFAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFAAFFFFF++FFF++F++FF–F–FF++F++FF–F–FF++F++FFFA |
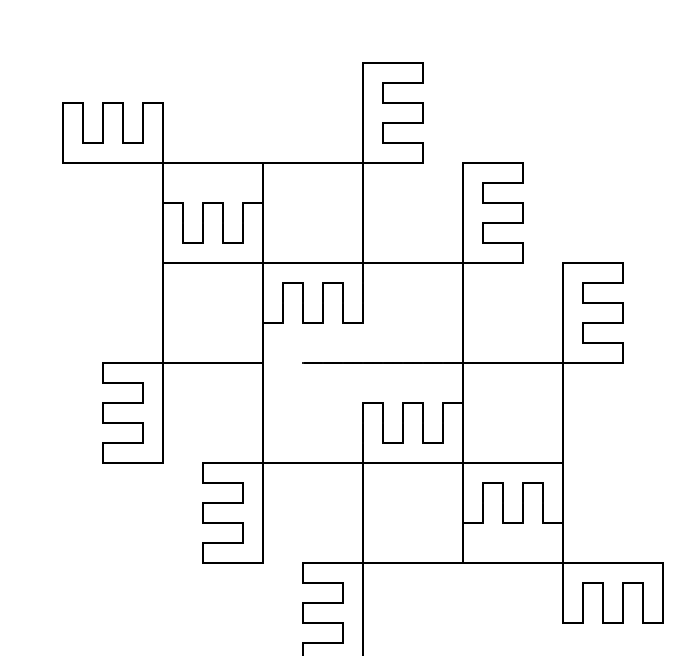
For my next design, I looked at the branching work in The Algorithmic Beauty of Plants. I specifically designed to see if I could implement circular berry-like bits to the end of the branches to make a berry bush.
| Design B | |
| Vocabulary | “F”, “B”, “+”, “-“, “[”, “]” |
| -> Variables | “F”, “B” |
| -> Constants | ”+”, “-“, “[”, “]” |
| Rules | (“F” -> “F[+FB]F[-F—-B]F”) |
| Axiom | “F[F][++F]–F” |
| Move Distance | 20 |
| Angle | 29.7 |
| Scale Factor | 0.5 |
| Drawing | “F” means move forward move distance |
| “B” means draw a circle in 360 segments of segment size 0.5 | |
| ”+” means turn right by angle | |
| ”-“ means turn left by angle | |
| ”[” means push the turtle state | |
| ”]” means pop the turtle state |
Iterations from n=0 to n=3
| Iteration (n) | Iteration String |
| 0 | F[F][++F]–F |
| 1 | F[+FB]F[-F—-B]F[F[+FB]F[-F—-B]F][++F[+FB]F[-F—-B]F]–F[+FB]F[-F—-B]F |
| 2 | F[+FB]F[-F—-B]F[+F[+FB]F[-F—-B]FB]F[+FB]F[-F—-B]F[-F[+FB]F[-F—-B]F—-B]F[+FB]F[-F—-B]F[F[+FB]F[-F—-B]F[+F[+FB]F[-F—-B]FB]F[+FB]F[-F—-B]F[-F[+FB]F[-F—-B]F—-B]F[+FB]F[-F—-B]F][++F[+FB]F[-F—-B]F[+F[+FB]F[-F—-B]FB]F[+FB]F[-F—-B]F[-F[+FB]F[-F—-B]F—-B]F[+FB]F[-F—-B]F]–F[+FB]F[-F—-B]F[+F[+FB]F[-F—-B]FB]F[+FB]F[-F—-B]F[-F[+FB]F[-F—-B]F—-B]F[+FB]F[-F—-B]F |
| 3 | F[+FB]F[-F—-B]F[+F[+FB]F[-F—-B]FB]F[+FB]F[-F—-B]F[-F[+FB]F[-F—-B]F—-B]F[+FB]F[-F—-B]F[+F[+FB]F[-F—-B]F[+F[+FB]F[-F—-B]FB]F[+FB]F[-F—-B]F[-F[+FB]F[-F—-B]F—-B]F[+FB]F[-F—-B]FB]F[+FB]F[-F—-B]F[+F[+FB]F[-F—-B]FB]F[+FB]F[-F—-B]F[-F[+FB]F[-F—-B]F—-B]F[+FB]F[-F—-B]F[-F[+FB]F[-F—-B]F[+F[+FB]F[-F—-B]FB]F[+FB]F[-F—-B]F[-F[+FB]F[-F—-B]F—-B]F[+FB]F[-F—-B]F—-B]F[+FB]F[-F—-B]F[+F[+FB]F[-F—-B]FB]F[+FB]F[-F—-B]F[-F[+FB]F[-F—-B]F—-B]F[+FB]F[-F—-B]F[F[+FB]F[-F—-B]F[+F[+FB]F[-F—-B]FB]F[+FB]F[-F—-B]F[-F[+FB]F[-F—-B]F—-B]F[+FB]F[-F—-B]F[+F[+FB]F[-F—-B]F[+F[+FB]F[-F—-B]FB]F[+FB]F[-F—-B]F[-F[+FB]F[-F—-B]F—-B]F[+FB]F[-F—-B]FB]F[+FB]F[-F—-B]F[+F[+FB]F[-F—-B]FB]F[+FB]F[-F—-B]F[-F[+FB]F[-F—-B]F—-B]F[+FB]F[-F—-B]F[-F[+FB]F[-F—-B]F[+F[+FB]F[-F—-B]FB]F[+FB]F[-F—-B]F[-F[+FB]F[-F—-B]F—-B]F[+FB]F[-F—-B]F—-B]F[+FB]F[-F—-B]F[+F[+FB]F[-F—-B]FB]F[+FB]F[-F—-B]F[-F[+FB]F[-F—-B]F—-B]F[+FB]F[-F—-B]F][++F[+FB]F[-F—-B]F[+F[+FB]F[-F—-B]FB]F[+FB]F[-F—-B]F[-F[+FB]F[-F—-B]F—-B]F[+FB]F[-F—-B]F[+F[+FB]F[-F—-B]F[+F[+FB]F[-F—-B]FB]F[+FB]F[-F—-B]F[-F[+FB]F[-F—-B]F—-B]F[+FB]F[-F—-B]FB]F[+FB]F[-F—-B]F[+F[+FB]F[-F—-B]FB]F[+FB]F[-F—-B]F[-F[+FB]F[-F—-B]F—-B]F[+FB]F[-F—-B]F[-F[+FB]F[-F—-B]F[+F[+FB]F[-F—-B]FB]F[+FB]F[-F—-B]F[-F[+FB]F[-F—-B]F—-B]F[+FB]F[-F—-B]F—-B]F[+FB]F[-F—-B]F[+F[+FB]F[-F—-B]FB]F[+FB]F[-F—-B]F[-F[+FB]F[-F—-B]F—-B]F[+FB]F[-F—-B]F]–F[+FB]F[-F—-B]F[+F[+FB]F[-F—-B]FB]F[+FB]F[-F—-B]F[-F[+FB]F[-F—-B]F—-B]F[+FB]F[-F—-B]F[+F[+FB]F[-F—-B]F[+F[+FB]F[-F—-B]FB]F[+FB]F[-F—-B]F[-F[+FB]F[-F—-B]F—-B]F[+FB]F[-F—-B]FB]F[+FB]F[-F—-B]F[+F[+FB]F[-F—-B]FB]F[+FB]F[-F—-B]F[-F[+FB]F[-F—-B]F—-B]F[+FB]F[-F—-B]F[-F[+FB]F[-F—-B]F[+F[+FB]F[-F—-B]FB]F[+FB]F[-F—-B]F[-F[+FB]F[-F—-B]F—-B]F[+FB]F[-F—-B]F—-B]F[+FB]F[-F—-B]F[+F[+FB]F[-F—-B]FB]F[+FB]F[-F—-B]F[-F[+FB]F[-F—-B]F—-B]F[+FB]F[-F—-B]F |
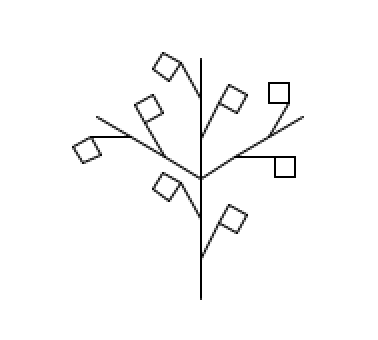
For Design C, I did some similar experiments with branching except drawing square polygons at the end of the branches.
| Design B | |
| Vocabulary | “F”, “C”, “+”, “-“, “[”, “]” |
| -> Variables | “F”, “C” |
| -> Constants | ”+”, “-“, “[”, “]” |
| Rules | (“F” -> “F[+FC]F[-F—-C]F”) |
| Axiom | “F[F][++F]–F” |
| Move Distance | 20 |
| Angle | 29.7 |
| Scale Factor | 0.5 |
| Drawing | “F” means move forward move distance |
| “C” means draw a square | |
| ”+” means turn right by angle | |
| ”-“ means turn left by angle | |
| ”[” means push the turtle state | |
| ”]” means pop the turtle state |
Iterations from n=0 to n=3
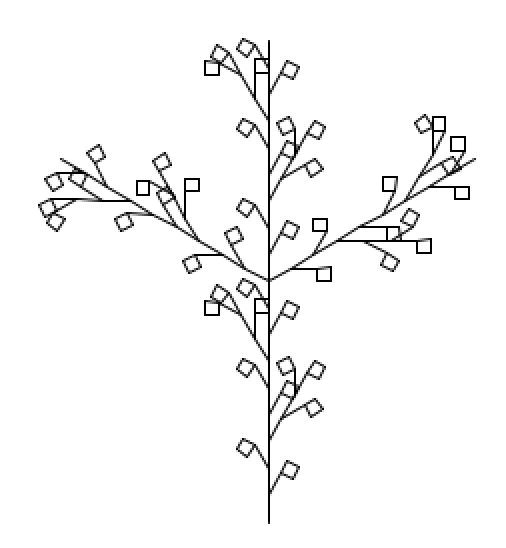

| Iteration (n) | Iteration String |
| 0 | F[F][++F]–F |
| 1 | F[+FC]F[-F—-C]F[F[+FC]F[-F—-C]F][++F[+FC]F[-F—-C]F]–F[+FC]F[-F—-C]F |
| 2 | F[+FC]F[-F—-C]F[+F[+FC]F[-F—-C]FC]F[+FC]F[-F—-C]F[-F[+FC]F[-F—-C]F—-C]F[+FC]F[-F—-C]F[F[+FC]F[-F—-C]F[+F[+FC]F[-F—-C]FC]F[+FC]F[-F—-C]F[-F[+FC]F[-F—-C]F—-C]F[+FC]F[-F—-C]F][++F[+FC]F[-F—-C]F[+F[+FC]F[-F—-C]FC]F[+FC]F[-F—-C]F[-F[+FC]F[-F—-C]F—-C]F[+FC]F[-F—-C]F]–F[+FC]F[-F—-C]F[+F[+FC]F[-F—-C]FC]F[+FC]F[-F—-C]F[-F[+FC]F[-F—-C]F—-C]F[+FC]F[-F—-C]F |
| 3 | F[+FC]F[-F—-C]F[+F[+FC]F[-F—-C]FC]F[+FC]F[-F—-C]F[-F[+FC]F[-F—-C]F—-C]F[+FC]F[-F—-C]F[+F[+FC]F[-F—-C]F[+F[+FC]F[-F—-C]FC]F[+FC]F[-F—-C]F[-F[+FC]F[-F—-C]F—-C]F[+FC]F[-F—-C]FC]F[+FC]F[-F—-C]F[+F[+FC]F[-F—-C]FC]F[+FC]F[-F—-C]F[-F[+FC]F[-F—-C]F—-C]F[+FC]F[-F—-C]F[-F[+FC]F[-F—-C]F[+F[+FC]F[-F—-C]FC]F[+FC]F[-F—-C]F[-F[+FC]F[-F—-C]F—-C]F[+FC]F[-F—-C]F—-C]F[+FC]F[-F—-C]F[+F[+FC]F[-F—-C]FC]F[+FC]F[-F—-C]F[-F[+FC]F[-F—-C]F—-C]F[+FC]F[-F—-C]F[F[+FC]F[-F—-C]F[+F[+FC]F[-F—-C]FC]F[+FC]F[-F—-C]F[-F[+FC]F[-F—-C]F—-C]F[+FC]F[-F—-C]F[+F[+FC]F[-F—-C]F[+F[+FC]F[-F—-C]FC]F[+FC]F[-F—-C]F[-F[+FC]F[-F—-C]F—-C]F[+FC]F[-F—-C]FC]F[+FC]F[-F—-C]F[+F[+FC]F[-F—-C]FC]F[+FC]F[-F—-C]F[-F[+FC]F[-F—-C]F—-C]F[+FC]F[-F—-C]F[-F[+FC]F[-F—-C]F[+F[+FC]F[-F—-C]FC]F[+FC]F[-F—-C]F[-F[+FC]F[-F—-C]F—-C]F[+FC]F[-F—-C]F—-C]F[+FC]F[-F—-C]F[+F[+FC]F[-F—-C]FC]F[+FC]F[-F—-C]F[-F[+FC]F[-F—-C]F—-C]F[+FC]F[-F—-C]F][++F[+FC]F[-F—-C]F[+F[+FC]F[-F—-C]FC]F[+FC]F[-F—-C]F[-F[+FC]F[-F—-C]F—-C]F[+FC]F[-F—-C]F[+F[+FC]F[-F—-C]F[+F[+FC]F[-F—-C]FC]F[+FC]F[-F—-C]F[-F[+FC]F[-F—-C]F—-C]F[+FC]F[-F—-C]FC]F[+FC]F[-F—-C]F[+F[+FC]F[-F—-C]FC]F[+FC]F[-F—-C]F[-F[+FC]F[-F—-C]F—-C]F[+FC]F[-F—-C]F[-F[+FC]F[-F—-C]F[+F[+FC]F[-F—-C]FC]F[+FC]F[-F—-C]F[-F[+FC]F[-F—-C]F—-C]F[+FC]F[-F—-C]F—-C]F[+FC]F[-F—-C]F[+F[+FC]F[-F—-C]FC]F[+FC]F[-F—-C]F[-F[+FC]F[-F—-C]F—-C]F[+FC]F[-F—-C]F]–F[+FC]F[-F—-C]F[+F[+FC]F[-F—-C]FC]F[+FC]F[-F—-C]F[-F[+FC]F[-F—-C]F—-C]F[+FC]F[-F—-C]F[+F[+FC]F[-F—-C]F[+F[+FC]F[-F—-C]FC]F[+FC]F[-F—-C]F[-F[+FC]F[-F—-C]F—-C]F[+FC]F[-F—-C]FC]F[+FC]F[-F—-C]F[+F[+FC]F[-F—-C]FC]F[+FC]F[-F—-C]F[-F[+FC]F[-F—-C]F—-C]F[+FC]F[-F—-C]F[-F[+FC]F[-F—-C]F[+F[+FC]F[-F—-C]FC]F[+FC]F[-F—-C]F[-F[+FC]F[-F—-C]F—-C]F[+FC]F[-F—-C]F—-C]F[+FC]F[-F—-C]F[+F[+FC]F[-F—-C]FC]F[+FC]F[-F—-C]F[-F[+FC]F[-F—-C]F—-C]F[+FC]F[-F—-C]F |
Task 4: Fabricate Your L-Systems
I designed to fabricate my A and B designs. A being squareish with 90 angle adjustments and B being my first branching structure with circles. The results were OK. One thing I did notice is that my naive approach to circles (drawing 360 line segments) resulted in my design taking a very very long time to create the print job. That design also generated a bit of a larger flame that singed my acrylic. I’m guessing it’s from the line segments used to make the circles. Other than that both pieces did engrave as I expected on acrylic.


Task 5: Probalistic L-Systems
I decided to take my design B (branching with circles) and try to make a new subclass with random distances and angles per iteration of parsing the current string. I had to play around with the random range for the angle and distances because certain values would make it so the branching plant-like look of the lsystem would be lost.
The parameters are the same as Task 3, Design B except the moveDistance is a random value between 5 and the given move distance, and the angle is in the range of angle - 2, angle + 2.
Here are three different runs of the same Design B with randomness at iteration n=4. It’s quite nice how much more varied the designs are compared to the original and also interesting how different the three designs are.
I implemented this code in my new ProbalisticLSystem.pde file and tested it with a clone of my Design B labeled D in initD() in the ExampleLSystemDesigns.pde.



I decided to skip doing the probalistic rules for now.
Mini #2 - “Lasered!” - Sunday, September 22, 2024
Assignment Description
Get comfortable with generating designs and going through a CAD/CAM workflow to fabricate them as physical objects. We used laser cutters in this specific case and tried out cutting and etching on a medium fo our choice.
Task 1: Generating Designs with Processing Functions
I enjoyed the content in our course going over how to generate basic designs in Processing. I recently took a Computer Graphics course where we primarily coded up our solutions in C using OpenGL frameworks and the difference between that and Processing is pretty stark. The amount of boilerplate code to get any OpenGL scene to render is significant so I can really appreciate how quickly you can prototype using Processing.
I primarily played around with concepts from Turtle Geometry: The Computer as a Medium for Exploring Mathematics.
Starting with some very basic rectangles along with basic turtle rotations you can get some pretty petal-like designs. The turtle geometry is much easier for me to conceptualize than only using cartesian coordinates. Here is the code for a basic attempt at a flower with petals. I had to experiment a bit with the loop iterations to make sure there was a complete rotation, but also a bit of a dense center to simulate how sunflowers look.
import Turtle.*;
Turtle t;
void setup() {
size(700, 700);
background(255);
stroke(0);
t = new Turtle(this);
noLoop();
}
void squarepiece(Turtle t, int size) {
t.forward(size);
t.right(90);
}
void rectangle(Turtle t, int side1, int side2) {
for (int i = 0; i < 2; i += 1) {
squarepiece(t, side1);
squarepiece(t, side2);
}
}
void draw() {
for (int i = 0; i < 40; i += 1) {
rectangle(t, 90, 10);
t.right(10);
}
}
The result doesn’t look too bad.
The Turtle book goes through some more interesting concepts like generating new poly objects that have behaviors like eventually having closed loops. Specifically working through adapting to have double iterations of a drawn vector (duopoly in the book) I could see really interesting shapes generate from different input values. The amount of change between input values could be very different and I eventually settled on using birthdays of myself, my partner, and my child to get three very different shapes. I did some tweaking using setX and setY so that objects could align together in a way that was easy to etch on some acrylic.
The code for duopoly:
import Turtle.*;
Turtle t;
void setup() {
size(1000, 1000);
background(255);
stroke(0);
t = new Turtle(this);
noLoop();
}
void vector(Turtle t, int direction, int length) {
t.setHeading(direction);
t.forward(length);
}
void duopoly(Turtle t, int side1, int angle1, int side2, int angle2) {
int c = 0;
for (int i = 0; i < 600; i++) {
vector(t, (c * angle1), side1);
vector(t, (c * angle2), side2);
c += 1;
}
}
void draw() {
t.setX(width/3);
t.setY(height/2);
duopoly(t, 19, 84, 4, 1); // Run duo poly using Matt Zago's birthday
t.setX(width/2);
t.setY(height/2);
duopoly(t, 19, 85, 8, 8); // Wife's birthday
duopoly(t, 20, 21, 3, 13); // Kiddo birthday
}
After playing with Turtle Geometry I decided to look at Processing’s reference library to see what you can do that’s more similar to the OpenGL rendering pipeline and discovered you can assemble a shape from vertices and drawn curves. I started with a basic grid with circles and then decided to try to make holes randomly generated radii that would make spark-like outlines.
void setup() {
size(600, 600);
background(255);
stroke(0);
noLoop();
}
void deformedCircle(int centerX, int centerY) {
int numPoints = 50;
float[] radii = new float[numPoints];
for (int i = 0; i < numPoints; i++) {
radii[i] = random(10,30);
}
beginShape();
for (int j = 0; j < numPoints; j++) {
float angle = map(j, 0, numPoints, 0, TWO_PI);
float x = centerX + (radii[j] * cos(angle));
float y = centerY + (radii[j] * sin(angle));
curveVertex(x,y);
}
endShape(CLOSE);
}
void draw() {
// Outline that will get cut
rect(100, 100, 400, 400);
// Draw in the grid
for (int i = 100; i <= 400; i += 100) {
for (int j = 100; j <= 400; j += 100) {
deformedCircle(i + 50, j + 50);
}
}
}

Task 2 - Fabricating Your Designs with Laser Cutting
I decided to use CU’s ITLL laser cutters and a bit out of laziness I went with acrylic because they sell nice 11x18” sheets to fabricate. I went ahead and fabricated my duopoly and deformed circle designs and I was happy with the results.
The biggest learning curve was just making sure the objects aligned with the acrylic and I had some issues with my pdf/svg exports of the deformed circles showing a large filled black outline until I removed that layer.
I was afraid when printing my deformed circles that the size of the circles were too small and that the acrylic would crack or not have the accuracy to draw the small radii, but my first print came out great.


Mini #1 - “Seeing is Believing” - Sunday, September 8, 2024
Assignment Description
The stated goal of our first assignment is to practice recognizing computational design. We’re encouraged to find different examples and show what we found.
Computational Design in Nature
Botanical World
I spent some time looking over different plant structures. I saw a lot of examples of fractal designs of leaves, but a plant I found pretty interesting is a succulent variety called the trachyandra. I was looking over examples and find the ribbon-like shapes to be intriguing. I’m sure there’s a computational way to generate psuedo-random ribbon-like structures that mimic this.
Here’s an image that I found looking over the succulentsnetwork’s site.

Zoological World
Growing up in Colorado, I’d see butterfly migrations occasionally. I was always partial to monarch butterflies like this example from Wikimedia. I was reading a bit more about butterfly anatomy on biologyinsights.com and that site uses the analogy of roof shingles for how the wing structure looks to overlap. I’m sure there are techniques to try to randomize the shape of the individual cell in the wing, overlap them, and then only provide the view of the overlapped cells to laser print, etc.

Environment Built by (non-human) Organisms
I was looking for different nests through your typical searches for intricate or strange birds nests and came upon the baya weaver from South East Asia. Wikipedia comes through with a good example picture of it seen here:

You can see across many birds nests that the instint of birds to use certain materials found around them and proceduraly create their nests is very algorithmic. There’s slight variation, but because of their consistent use of certain materials the nests look common to their environment and breed. There might be some strange birds out there that buck this trend, but I didn’t go that deep into it. I’m not actually sure what the best approach is to programmatically generate a birds nest. I wish I knew more about the structural integrity of nests and how birds decide a nest is finished or not to try to mock up a bird nest creating algorithm.
Computational Design in the Human-made Built Environment
The University of Stuttgart has a really nice example of computational fabrication and design with their IBA Timber House. At a high-level it’s a structure that attempts to mimic a log cabin except on its side. But what’s interesting is they computationally designed the joints to use natural materials to connect the staggered timber that makes the building so unique.

You can see the popularity of 3d-printed materials in places like the Moma Design Store (Moma is one of the more popular design museums in New York City). They try to use sustainable materials, but the planters have the 3d-printed design aesthetic on purpose.

There’s interesting examples in the world of fashion as well with computational designed dresses like this one:

Two Human Practitioners of Computational Fabrication
I came across Neri Oxman. In particular one of her works named Silk Pavillion II is very intriguing. It uses a kinetic jig to move around a soluble knit where live silkworms create the structure. The combination of organic living creatures, silk worms, with guided assistance by jig along with sensors makes for a very compelling combination. It wouldn’t be nearly as interesting if she only used the silk worms with something static or only used cnc or robotic loom techniques to construct the pavillion without the worms.

Michael Hansmeyer is a really interesting architect who uses algorithmic approaches to create new structures. I was looking at his White Tower (Tor Alva) that’s being built in Switzerland. He used a concrete extrusion process which uses a lot of normal 3d printing techniques except at a much larger scale.

An Intro - Monday, August 26, 2024
This is a running journal of thoughts while working through content on computational fabrication during enrollment at University of Colorado at Boulder’s CSCI 7000 course. I can’t recall making much with my hands since making a CD rack back in middle school machine shop class, and I’m quite excited to get started making things at the Blow Things Up Lab.
While preparing for first class, I went through some course materials to install Processing. I went through creating some basic sketches and looking at Orthogonal and Perspective views of cubes. I just finished a Computer Graphics course in the summer where we wrote a few thousand lines of C code and uses OpenGL APIs to do some basic things, and Processing’s learning curve is hilariously small compared to the basics to get a black window, cube, perspective camera, and lighting working in OpenGL. The usage of Java is a bit uncomfortable for me because I haven’t done much with Java in about a decade, but the initial sketches don’t really involve much more than function calling and some basic imports so overall I’m not that worried.